题目内容
2.已知△ABC是等边三角形,椭圆Γ的一个焦点为A,另一个焦点F在线段BC上,如果椭圆Γ恰好经过B,C两点,则它的离心率为$\frac{\sqrt{3}}{3}$.分析 如图所示,不妨取BC⊥x轴,AC=2,可得2a=3,2c=$\sqrt{3}$,即可得出.
解答  解:如图所示
解:如图所示
不妨取BC⊥x轴,AC=2,
则2a=3,2c=$\sqrt{3}$,
∴$e=\frac{c}{a}$=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查了等边三角形的性质、椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
3.下列图示所表示的对应关系不是映射的是( )
| A. |  | B. |  | C. |  | D. |  |
10.若cos2θ+cosθ=0,则sin2θ+sinθ的值等于( )
| A. | 0 | B. | ±$\sqrt{3}$ | C. | 0或$\sqrt{3}$ | D. | 0或±$\sqrt{3}$ |
7.一个三棱锥的三视图如图所示,则该三棱锥的表面积为( )
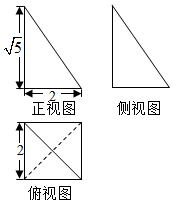

| A. | 8+$\sqrt{14}$ | B. | 8+2$\sqrt{14}$ | C. | 2+2$\sqrt{5}$+$\sqrt{14}$ | D. | 16+2$\sqrt{14}$ |