Question

在△ABC中,已知AB=,cosB=,AC边上的中线BD=,求sinA的值.

Answer 1

解法一：设E为BC的中点,连结DE,则DE∥AB,且DE=AB=,设BE=x.

    在△BDE中利用余弦定理可得BD²=BE²+ED²-2BE·EDcos∠BED,

5=x²++2××x,

    解得x=1,x=(舍去).

    故BC=2,从而AC²=AB²+BC²-2AB·BCcosB=,即AC=.

    又sinB=,故=,sinA=.

解法二：以B为坐标原点, 为x轴正向建立直角坐标系,且不妨设点A位于第一象限.

    由sinB=,则=(cosB,sinB)=(,).

    设=(x,0),则=(,).

    由条件得||==.

    从而x=2,x=-(舍去).

    故=(-,).

    于是cosA==,

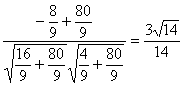∴sinA==.

解法三：过A作AH⊥BC交BC于H,延长BD到P使BD=DP,连结AP、PC.

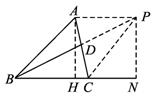
    过P作PN⊥BC交BC的延长线于N,则HB=ABcosB=,AH=.

BN====,而CN=HB=,

∴BC=BN-CN=2,HC=,AC==.

    故由正弦定理得=,

∴sinA=.