题目内容
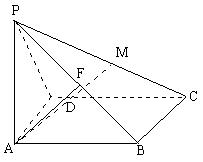
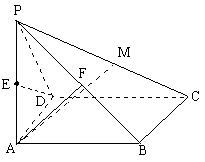 如图四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,AB=2,PC与平面ABCD成45°角,E、F分别为PA、PB的中点.
如图四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,AB=2,PC与平面ABCD成45°角,E、F分别为PA、PB的中点.
(1)求异面直线DE与AF所成角的大小;
(2)设M是PC上的动点,试问当M在何处时,才能使AM⊥平面PBD,证明你的结论.
【答案】
解:(1)如图,建立空间直角坐标系,则A(0,0,0),F(1,0, ),D(0,2,0),E(0,0,
),D(0,2,0),E(0,0, );
);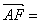 (1,0,
(1,0,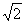 ),
),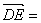 (0,-2,
(0,-2,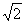 ).
).
设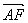 与
与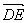 的夹角为θ,
的夹角为θ,
 则cos=
则cos=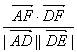 =
=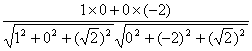 =
=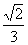 ,
,
∴DE与AF所成的角为arccos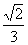 .
.
(2)∵PA⊥平面ABCD,∴PA⊥BD.
又ABCD是正方形,∴BD⊥AC,BD⊥平面PAC,∴BD⊥AM.
由题意可设M点坐标为(t,t,2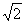 (2-t’),
(2-t’),
∴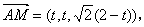 又P(0,0,2
又P(0,0,2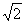 ),B(2,0,0),
),B(2,0,0),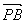 =(2,0,-2
=(2,0,-2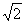 ).
).
设AM⊥PB,∴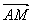 ·
· 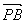 =0,即2t-2
=0,即2t-2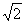 ×
×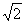 (2-t)=0.
(2-t)=0.
∴t=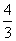 ,∴|
,∴|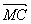 |=
|=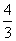 ,又|
,又|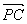 |=4,
|=4,
∴M在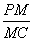 =2这位置于,AM⊥平面PBD.
=2这位置于,AM⊥平面PBD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
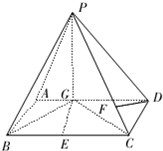 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且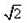 ,F是BC的中点.
,F是BC的中点.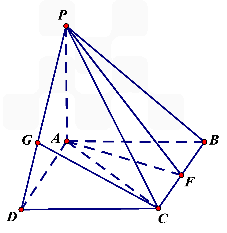
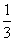 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.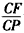 的值。
的值。 
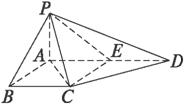
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.