Question

【题目】已知函数f（x）= ， g（x）=asin（x+π）﹣2a+2（a＞0），给出下列结论：
①函数f（x）的值域为[0，]；
②函数g（x）在[0，1]上是增函数；
③对任意a＞0，方程f（x）=g（x）在区间[0，1]内恒有解；
④若x1∈R，x2∈[0，1]，使得f（x1）=g（x2）成立，则实数a的取值范围是：≤a≤ ．
其中所有正确结论的序号为

Answer 1

【答案】①②④
【解析】当x≥1时，函数f（x）==
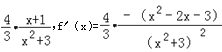
1≤x≤3时，f′（x）≥0，x≥3时，f′（x）≤0，故当x=3时，f（x）取极大值 ， 故此时f（x）∈[0，]，
当x≤1时，函数f（x）=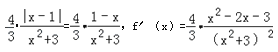
﹣1≤x≤1时，f′（x）≤0，x≤﹣1时，f′（x）≥0，故当x=﹣1时，f（x）取极大值 ， 故此时f（x）∈[0，]，
综上可得：函数f（x）的值域为[0，]；故①正确；
当x∈[0，1]时，x+π∈[π，]，此时函数g（x）为增函数，故②正确；
x∈[0，1]时，f（x）= ， 故f（x）为减函数，
由f（0）= ， f（1）=0，可得f（x）∈[0，]，
而g（0）=﹣3a+2，g（1）=-a+2，故g（x）∈[﹣3a+2，-a+2]，
当-a+2≥0，即a≤时，方程f（x）=g（x）有解，
当-a+2＜，即a＞时，方程f（x）=g（x）无解，故③错误；
若x1∈R，x2∈[0，1]，使得f（x1）=g（x2）成立，
则-a+2≥0，且﹣3a+2≤；
解得：≤a≤ ． 故④正确；
所以答案是：①②④，
【考点精析】掌握命题的真假判断与应用是解答本题的根本，需要知道两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．