题目内容
(本小题满分14分)
如图,已知椭圆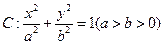 的离心率为
的离心率为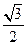 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为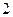 .设直线
.设直线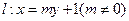 与椭圆
与椭圆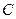 相交于
相交于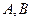 两点,点
两点,点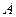 关于
关于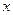 轴对称点为
轴对称点为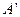 .
.
(1)求椭圆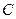 的方程;
的方程;
(2)若以线段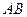 为直径的圆过坐标原点
为直径的圆过坐标原点
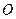 ,求直线
,求直线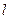 的方程;
的方程;
(3)试问:当 变化时,直线
变化时,直线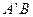 与
与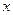 轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.

如图,已知椭圆
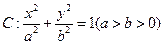 的离心率为
的离心率为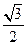 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为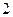 .设直线
.设直线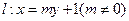 与椭圆
与椭圆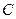 相交于
相交于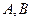 两点,点
两点,点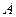 关于
关于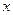 轴对称点为
轴对称点为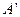 .
.(1)求椭圆
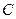 的方程;
的方程;(2)若以线段
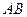 为直径的圆过坐标原点
为直径的圆过坐标原点
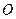 ,求直线
,求直线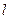 的方程;
的方程;(3)试问:当
 变化时,直线
变化时,直线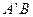 与
与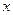 轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
解:(1)由题意可得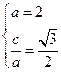 ,解得
,解得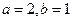
所以椭圆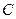 的方程为
的方程为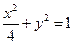 …………(4分)
…………(4分)
(2)由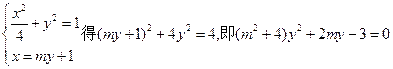
设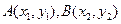 ,则
,则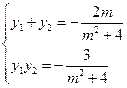 …………(5分)
…………(5分)
因为 以线段
以线段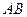 为直径的圆过坐标原点
为直径的圆过坐标原点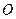 ,即
,即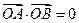
所以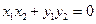 ,
,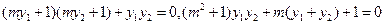
………………(7分)
所以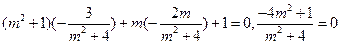
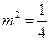 ,
,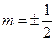
故所求直线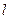 的方程为
的方程为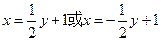 …………(9分)
…………(9分)
(3)由(2)知: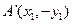
则直线 的方程为
的方程为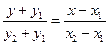 ,令
,令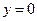 ,得…………(11分)
,得…………(11分)
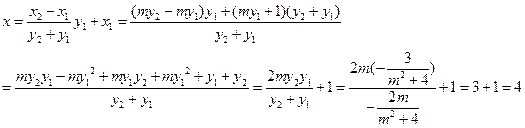
…………(13分)
这说明,当 变化时,直线
变化时,直线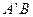 与
与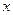 轴交于定点
轴交于定点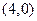 …………(
…………( 14分)
14分)
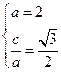 ,解得
,解得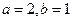
所以椭圆
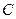 的方程为
的方程为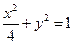 …………(4分)
…………(4分)(2)由
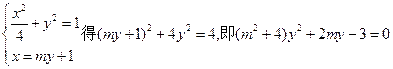
设
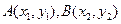 ,则
,则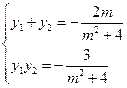 …………(5分)
…………(5分)因为
 以线段
以线段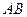 为直径的圆过坐标原点
为直径的圆过坐标原点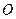 ,即
,即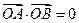
所以
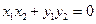 ,
,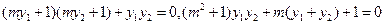
………………(7分)
所以
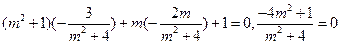
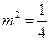 ,
,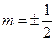
故所求直线
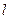 的方程为
的方程为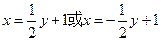 …………(9分)
…………(9分)(3)由(2)知:
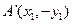
则直线
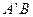 的方程为
的方程为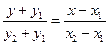 ,令
,令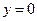 ,得…………(11分)
,得…………(11分)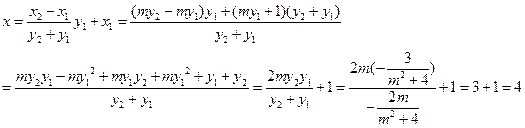
…………(13分)
这说明,当
 变化时,直线
变化时,直线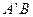 与
与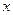 轴交于定点
轴交于定点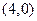 …………(
…………( 14分)
14分)略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
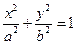 (a>b>0)的离心率
(a>b>0)的离心率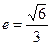 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为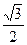 .
.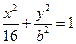
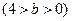 ,
,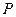 为椭圆上的动点,
为椭圆上的动点,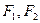 为椭圆的两焦点,当
为椭圆的两焦点,当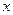 轴上时,过
轴上时,过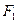 作
作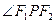 的外角平分线的垂线
的外角平分线的垂线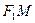 ,垂足为
,垂足为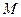 ,当点
,当点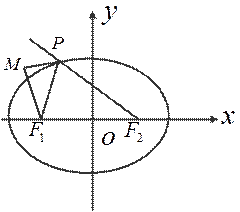
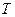 的方程;
的方程;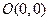 、
、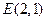 ,试探究是否存在这样的点
,试探究是否存在这样的点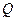 :点
:点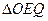 的面积
的面积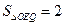 ?若存
?若存 在,求出点
在,求出点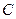 :
: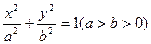 ,
,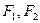 分别为左,右焦点,离心率为
分别为左,右焦点,离心率为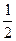 ,点
,点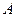 在椭圆
在椭圆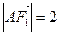 ,
,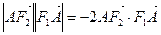 ,过
,过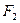 与坐标轴不垂直的直线
与坐标轴不垂直的直线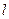 交椭圆于
交椭圆于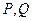 两点.
两点.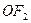 上是否存在点
上是否存在点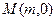 ,使得以线段
,使得以线段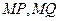 为邻边的四边形是菱形?若存在,求出实数
为邻边的四边形是菱形?若存在,求出实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. 椭圆
椭圆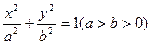 的左、右焦点分别为
的左、右焦点分别为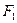 、
、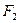 ,过
,过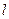 与椭圆相交于A、B
与椭圆相交于A、B 两点。
两点。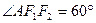 ,且
,且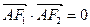 ,求椭圆的离心率;
,求椭圆的离心率;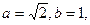 求
求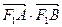 的最大值和最小值。
的最大值和最小值。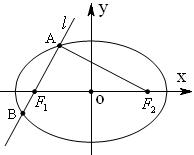
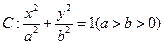 上的动点
上的动点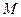 引
引 圆
圆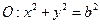 的两条切线
的两条切线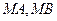 ,其中
,其中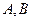 分别为切点,,若椭圆上存在点
分别为切点,,若椭圆上存在点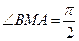 ,则该椭圆的离心率为____________.
,则该椭圆的离心率为____________.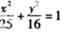 上一点P到其左准线的距离为10,F是该椭圆的左焦点,若点M满足
上一点P到其左准线的距离为10,F是该椭圆的左焦点,若点M满足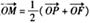 (其中O为坐标原点),则
(其中O为坐标原点),则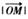 =_________
=_________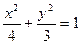 的长轴两端点为
的长轴两端点为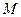 、
、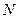 ,异于
,异于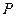 在椭圆上,则
在椭圆上,则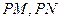 的斜率之积为 .
的斜率之积为 . ,-2),Q(-2
,-2),Q(-2