题目内容
设y=x2+mx+n（m、n∈R），当y=0时，对应x值的集合为{-2，-1}．
（1）求m、n的值；
（2）若x∈[-5，5]，求该函数的最值．
解：（1）y=0，即x2+mx+n=0，则x1=-1，x2=-2为其两根．
由韦达定理知：x1+x2=-2+（-1）=-3=-m，所以m=3．
x1•x2=-2×（-1）=2=n，所以n=2．
（2）由（1）知：
，因为x∈[-5，5]，
所以，当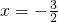
时，该函数取得最小值
．
又因为f（-5）=12，f（5）=42，所以当x=5时，该函数取得最大值f（x）max=f（5）=42
分析：（1）求出y=0的两个实数根，再利用一元二次方程的根与系数的关系，求得m、n的值．
（2）由二次函数的图象和性质，求得该函数的最值．
点评：本题主要考查求二次函数在闭区间上的最值，一元二次方程的根与系数的关系，属于中档题．
由韦达定理知：x1+x2=-2+（-1）=-3=-m，所以m=3．
x1•x2=-2×（-1）=2=n，所以n=2．
（2）由（1）知：
，因为x∈[-5，5]，所以，当
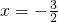时，该函数取得最小值．又因为f（-5）=12，f（5）=42，所以当x=5时，该函数取得最大值f（x）max=f（5）=42
分析：（1）求出y=0的两个实数根，再利用一元二次方程的根与系数的关系，求得m、n的值．
（2）由二次函数的图象和性质，求得该函数的最值．
点评：本题主要考查求二次函数在闭区间上的最值，一元二次方程的根与系数的关系，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目