Question

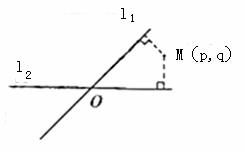
如下图，两条直线相交于O，夹角是60°，甲、乙两人分别在OX、OY上的A、B两点，|OA|=3 km,|OB|=1 km，两人同时都以4 km/h的速度行走，甲沿方向，乙沿方向，求：

（1）经过t h后，两人距离是多少（表示为t的函数）？

（2）何时两人距离最近？

Answer 1

解：(1)设经过t h后，甲、乙分别到达P、Q两点，则|AP|=4t，|BQ|=4t.

当t=时，P点与O点重合，故分两种情况讨论：

当t∈［0,］时，

|PQ|²=（3-4t）²+(1+4t)²-2(3-4t)(1+4t).cos60°=48t²-24t+7;

当t∈(,+∞)时，

|PQ|²=（4t-3）²+(1+4t)²-2(4t-3)(1+4t).cos120°=48t²-24t+7.

综上所述，|PQ|=(t≥0).

(2)当t= h时，两人距离最近,最近距离为2 km.