题目内容
如下图,两条异面直线AB、CD与三平行平面α、β、γ分别相交于A、E、B及C、F、D,又AD、BC与平面β的交点为H、G,求证:四边形EHFG为平行四边形.

答案:
解析:
解析:
证明:如题图所示,∵α∥β,
又平面ABC∩α=AC,平面ABC∩β=EG,
∴AC∥EG.同理AC∥HF,EG∥HF.
同理EH∥GF.
∴四边形EHFG为平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(1)
如下图是正方体的平面展开图,则在这个正方体中:|
①  平行. 平行. |
②  与 与 是异面直线. 是异面直线. |
|
③  与 与 成60°角. 成60°角. |
④  与 与 是异面直线. 是异面直线. |
以上四个命题中,正确命题的序号是
[
]|
(A) ①②③ |
(B) ②④ |
|
(C) ③④ |
(D) ②③④ |

(2)
如下图,正方体 中,
中, 的中点为
的中点为 ,
, 的中点为
的中点为 ,则异面直线
,则异面直线 与
与 所成的角是
所成的角是
[
]|
(A)0° |
(B)45° |
(C)60° |
(D)90° |

(3)
给出三个命题:①若两条直线和第三条直线所成的角相等,则这两条直线互相平行.
②若两条直线都与第三条直线垂直,则这两条直线互相平行.
③若两条直线都与第三条直线平行,则这两条直线互相平行.
其中不正确命题的个数是
[
]|
(A)0 |
(B)1 |
(C)2 |
(D)3 |

 ,
, ,
, 是三条直线,且
是三条直线,且 ∥
∥ ,
, 与
与 的夹角为
的夹角为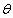 ,那么
,那么 与
与 夹角为______;
夹角为______;
 是长方体的一条棱,这个长方体中与
是长方体的一条棱,这个长方体中与 垂直的棱共______条;
垂直的棱共______条;

 ,
, 是异面直线,直线
是异面直线,直线 与
与 ,
,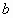 都相交,那么这三条直线中的两条所确定的平面共有_______个;
都相交,那么这三条直线中的两条所确定的平面共有_______个;
 ,
, ,
, ∥平面
∥平面 ,则
,则 与
与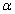 的位置关系是______;
的位置关系是______;
 ,
, 分别是长方体相邻两个面的对角线所在的直线,则
分别是长方体相邻两个面的对角线所在的直线,则 与
与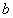 的位置关系是______.
的位置关系是______.