Question

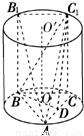
在圆柱OO′中，△ABC是其下底面的内接正三角形，B₁、C₁是其上底面的两点，且B₁B⊥平面ABC，C₁C⊥平面ABC．已知AB=2，AB₁=4．
（1）求几何体ABB₁C₁C与圆柱OO'的体积之比；
（2）当点D是AC中点时，证明：AB₁∥平面BDC₁，并求二面角D-BC₁-C的余弦值．

Answer 1

【答案】分析：（1）由B₁B⊥平面ABC，AB?平面ABC，知B₁B⊥AB．在Rt△ABB₁中，AB=2，AB₁=4，故，作AM⊥BC于M，在正△ABC中，AM=，底面半径，，，由此能求出几何体ABB₁C₁C与圆柱OO'的体积之比．
（2）连接B₁C交BC₁于点E，连接DE．于是E为B₁C的中点，而D为AC中点，DE∥AB₁，由此能够证明AB∥平面BDC₁．以B为原点，BC为y轴，BB₁为z轴，建立空间直角坐标系，则，，得到平面BDC₁的法向量，，平面BCC₁的法向量，由此能求出二面角D-BC₁-C的余弦值．
解答：解：（1）∵B₁B⊥平面ABC，AB?平面ABC，
∴B₁B⊥AB．
在Rt△ABB₁中，AB=2，AB₁=4，
∴，
作AM⊥BC于M，
在正△ABC中，AM=，
∴底面半径，，
∵，
∴几何体ABB₁C₁C与圆柱OO'的体积之比：
=．
（2）连接B₁C交BC₁于点E，连接DE．
于是E为B₁C的中点，
而D为AC中点，
∴DE是△AB₁C的中位线，
∴DE∥AB₁，
∵DE?平面BDC₁，AB?平面BDC₁，
∴AB∥平面BDC₁．
以B为原点，BC为y轴，BB₁为z轴，建立如图所示的空间直角坐标系，
则B（0，0，0），D（），，
∴，，
设为平面BDC₁的法向量，
则，∴∴，
∵平面BCC₁的法向量，
设二面角D-BC₁-C的平面角为θ，
则cosθ==．
点评：本题考查立体几何的综合运用，考查运算求解能力，推理论证能力；考查化归与转化思想．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答．