题目内容
已知数列{an}中,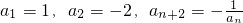 ,Sn是数列{an}的前n项和,则S2010=________.
,Sn是数列{an}的前n项和,则S2010=________.
-754
分析:列出数列的前几项,发现数列{an}是周期为4的周期数列.因此只要将S2010表示成前4项和的502倍,再加上a1+a2的值,即可得到它的值.
解答:∵ ,
,
∴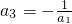 =-1,
=-1,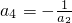 =
= ,
,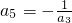 =1=a1,
=1=a1, =-2=a2,…
=-2=a2,…
由此发现,数列{an}满足 ,是周期为4的周期数列.
,是周期为4的周期数列.
∴S2010=(a1+a2+a3+a4)+(a5+a6+a7+a8)+…+(a2005+a2006+a2007+a2008)+a2009+a2010
=502(a1+a2+a3+a4)+(a1+a2)=502(1-2-1+ )+(1-2)=-754
)+(1-2)=-754
故答案为:-754
点评:本题给出数列的前2项和递推公式,叫我们求它的2010项的和,考查了进行简单的合情推理和数列求和等知识,属于基础题.
分析:列出数列的前几项,发现数列{an}是周期为4的周期数列.因此只要将S2010表示成前4项和的502倍,再加上a1+a2的值,即可得到它的值.
解答:∵
 ,
,∴
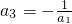 =-1,
=-1,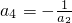 =
= ,
,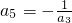 =1=a1,
=1=a1, =-2=a2,…
=-2=a2,…由此发现,数列{an}满足
 ,是周期为4的周期数列.
,是周期为4的周期数列.∴S2010=(a1+a2+a3+a4)+(a5+a6+a7+a8)+…+(a2005+a2006+a2007+a2008)+a2009+a2010
=502(a1+a2+a3+a4)+(a1+a2)=502(1-2-1+
 )+(1-2)=-754
)+(1-2)=-754故答案为:-754
点评:本题给出数列的前2项和递推公式,叫我们求它的2010项的和,考查了进行简单的合情推理和数列求和等知识,属于基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|