题目内容
 如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).
如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).(1)试求函数f(t)的解析式;
(2)画出函数y=f(t)的图象.
分析:(1)分情况讨论:当0≤t≤2时,所求面积等于四边形OABC的面积减去一三角形面积;当2<t≤5时,所求面积等于一矩形面积.
(2)根据各段函数表达式的特征分别画出即可.
(2)根据各段函数表达式的特征分别画出即可.
解答: (1)设直线x=t与x轴交于点D,与线段OA交于点E,与线段AB交于点F,
(1)设直线x=t与x轴交于点D,与线段OA交于点E,与线段AB交于点F,
则SOCBA=
×2×2+(5-2)×2=8,
①当0≤t≤2时,f(t)=SOCBA-S△ODE=8-
t2,
②当2<t≤5时,f(t)=SDCBF=(5-t)×2=10-2t,
所以f(t)=
.
(2)y=f(t)的图象如图所示:.
 (1)设直线x=t与x轴交于点D,与线段OA交于点E,与线段AB交于点F,
(1)设直线x=t与x轴交于点D,与线段OA交于点E,与线段AB交于点F,则SOCBA=
| 1 |
| 2 |
①当0≤t≤2时,f(t)=SOCBA-S△ODE=8-
| 1 |
| 2 |
②当2<t≤5时,f(t)=SDCBF=(5-t)×2=10-2t,
所以f(t)=
|
(2)y=f(t)的图象如图所示:.
点评:本题考查函数解析式的求法及简单函数的图象,注意分类讨论思想在本题中的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
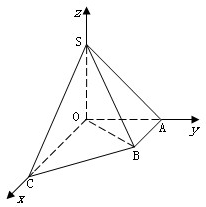 如图直角梯形OABC中,∠COA=∠OAB=
如图直角梯形OABC中,∠COA=∠OAB=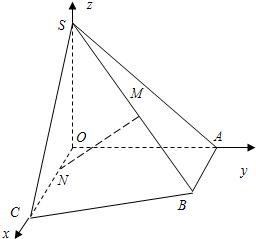 如图所示在直角梯形OABC中,∠COA=∠OAB=
如图所示在直角梯形OABC中,∠COA=∠OAB= 如图所示,在直角梯形OABC中,
如图所示,在直角梯形OABC中,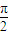 ,OA=OS=AB=1,OC=4,
,OA=OS=AB=1,OC=4,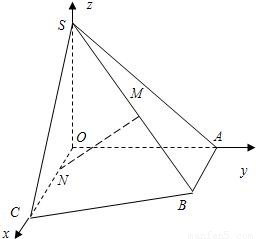
 ,OA=OS=AB=1,OC=4,
,OA=OS=AB=1,OC=4,