Question

规定A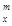=x(x-1)…(x-m+1)，其中x∈R，m为正整数，且A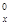=1，这是排列数A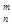(n，m是正整数，且m≤n)的一种推广．

  （1）求A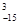的值；

  （2）排列数的性质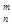：A=nA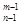 (其中m，n是正整数)．问是否都能推广到A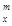(x∈R，m是正整数)的情形?若能推广，写出推广的形式，并且给予证明。

 

Answer 1

【答案】

(1)=(-15)(-16)(-17)=   - 4080；                             

(2)性质可推广，推广的形式分别是

，事实上，当m=1时，左边==x，右边=x=x，等式成立；  

当m≥2时，左边=x(x-1)(x-2)…(x-m+1)=x{(x-1)(x-2)…[(x-1)-(m-1)+1]}=x，

因此，成立；

【解析】略