题目内容
求证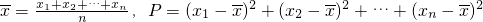
，q=（x1-a）2+（x2-a）2+…+（xn-a）2若
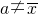则一定有
- A.P＞q
- B.P＜q
- C.P、q的大小不定
- D.以上都不对
B
分析：设f（x）=（x1-x）2+（x2-x）2+…+（xn-x）2，将此式化成二次函数的一般形式，结合二次函数的最值即可进行判定．
解答：设f（x）=（x1-x）2+（x2-x）2+…+（xn-x）2，
则f（x）=nx2-2（x1+x2+…+xn）x+x12+x22+…+xn2
当
时，f（x）取得最小值，
即P＜q．
故选B．
点评：本题主要考查了二次函数在函数极值中的应用，解答的关键是利用函数思想结合二次函数的最值即可．
分析：设f（x）=（x1-x）2+（x2-x）2+…+（xn-x）2，将此式化成二次函数的一般形式，结合二次函数的最值即可进行判定．
解答：设f（x）=（x1-x）2+（x2-x）2+…+（xn-x）2，
则f（x）=nx2-2（x1+x2+…+xn）x+x12+x22+…+xn2
当
时，f（x）取得最小值，即P＜q．
故选B．
点评：本题主要考查了二次函数在函数极值中的应用，解答的关键是利用函数思想结合二次函数的最值即可．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
求证
=
，P=(x1-
)2+(x2-
)2+…+(xn-
)2，q=（x1-a）2+（x2-a）2+…+（xn-a）2若a≠
则一定有（ ）
. |
| x |
| x1+x2+…+xn |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
| A、P＞q | B、P＜q |
| C、P、q的大小不定 | D、以上都不对 |
，q=（x1-a）2+（x2-a）2+…+（xn-a）2若
则一定有（ ）