题目内容
有一个不透明的袋子,装有4个完全相同的小球,球上分别编有数字1,2,3,4.
(Ⅰ)若逐个不放回取球两次,求第一次取到球的编号为偶数且两个球的编号之和能被3整除的概率;
(Ⅱ)若先从袋中随机取一个球,该球的编号为a,将球放回袋中,然后再从袋中随机取一个球,该球的编号为b,求直线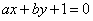 与圆
与圆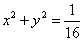 有公共点的概率.
有公共点的概率.
解:(I)用(a,b)(a表示第一次取到球的编号,b表示第二次取到球的编号)表示先后二次取球构成的基本事件,则基本事件有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12个.
设“第一次取到球的编号为偶数且两个球的编号之和能被3整除”为事件A,
则事件A包含的基本事件有:(2,1),(2,4),(4,2)共有3个,
∴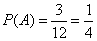
(II)基本事件有(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共16个,
设“直线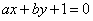 与圆
与圆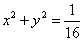 有公共的”为事件B,由题意
有公共的”为事件B,由题意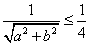 ,
,
即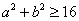 ,则事件B包含的基本事件有(1,4),(2,4),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共8个,
,则事件B包含的基本事件有(1,4),(2,4),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共8个,
∴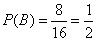 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,若
中,若 ,则有
,则有
 成立.类比上述性质,在等比数列
成立.类比上述性质,在等比数列 中,若
中,若 ,则有 .
,则有 .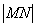 的最大值为
的最大值为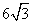 (B)
(B) 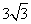 (C)
(C) 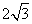 (D)3
(D)3 ,运算原理如图所示,则式子
,运算原理如图所示,则式子 的值为
的值为  内随机取两个数a、b, 则使得函数
内随机取两个数a、b, 则使得函数 有零点的概率为 .
有零点的概率为 . ,这条高与底边的夹角为
,这条高与底边的夹角为 ,则底边长为
,则底边长为 B.
B. C.
C. D.
D.
 的最大值是
的最大值是 ,最小值为
,最小值为 ,则
,则  B.
B. C.
C. D.
D.
 是正
是正 三边的中点,由
三边的中点,由 六点中的两点构成的向量中与
六点中的两点构成的向量中与 共线(
共线( .
.
 .
.
 .
.
 .
.

 ( )
( )






