题目内容
已知 且
且 ,设
,设 ,
,  .(1)试求
.(1)试求 的系数的最小值;
的系数的最小值;
(2)对于使 的系数为最小的
的系数为最小的 ,求此时
,求此时 的近似值(精确到0.01).
的近似值(精确到0.01).
 且
且 ,设
,设 ,
,  .(1)试求
.(1)试求 的系数的最小值;
的系数的最小值;(2)对于使
 的系数为最小的
的系数为最小的 ,求此时
,求此时 的近似值(精确到0.01).
的近似值(精确到0.01).(1)9;(2)2.02.
本试题主要考查了二项式定理的展开式通项公式的运用。
(1)中因为
 且
且 ,设
,设 ,
,  .
.
当m=3,n=4是 系数最小值为9 -------------8分
系数最小值为9 -------------8分
(2)中则使 的系数为最小的
的系数为最小的 ,求此时
,求此时 的近似值2.02 ------------6分
的近似值2.02 ------------6分
解:(1)因为
 且
且 ,设
,设 ,
,  .
.
当m=3,n=4是 系数最小值为9 -------------8分
系数最小值为9 -------------8分
(2)则使 的系数为最小的
的系数为最小的 ,求此时
,求此时 的近似值即为展开式中前几项的和也就是2.02 ------------6分
的近似值即为展开式中前几项的和也就是2.02 ------------6分
(1)中因为
 且
且 ,设
,设 ,
,  .
.当m=3,n=4是
 系数最小值为9 -------------8分
系数最小值为9 -------------8分(2)中则使
 的系数为最小的
的系数为最小的 ,求此时
,求此时 的近似值2.02 ------------6分
的近似值2.02 ------------6分解:(1)因为
 且
且 ,设
,设 ,
,  .
.当m=3,n=4是
 系数最小值为9 -------------8分
系数最小值为9 -------------8分(2)则使
 的系数为最小的
的系数为最小的 ,求此时
,求此时 的近似值即为展开式中前几项的和也就是2.02 ------------6分
的近似值即为展开式中前几项的和也就是2.02 ------------6分
练习册系列答案
相关题目
 ,则
,则 的值为
的值为



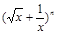 的展开式中各项系数和为64.
的展开式中各项系数和为64.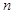 ;
; 的展开式的各项系数之和为
的展开式的各项系数之和为 ,二项式系数之和为
,二项式系数之和为 ,若
,若 ,则展开式中含
,则展开式中含 项的系数为( )
项的系数为( ) 展开式中各项的系数和为__________
展开式中各项的系数和为__________ 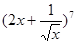 的二项展开式中
的二项展开式中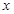 的系数是____ (用数学作答).
的系数是____ (用数学作答). 的展开式中,
的展开式中, 的系数是 。
的系数是 。 展开式中
展开式中 的系数为10, 则实数
的系数为10, 则实数 的值为
的值为  除以9以后的余数为___________________.
除以9以后的余数为___________________.