题目内容

已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的左顶点、上顶点分别为A、B，P为线段AB上一点，F1、F2分别为椭圆E的左、右焦点，若
PF1
•
PF2
的最小值小于零，则椭圆E的离心率的取值范围为（　　）
分析：依题意可求得AB的方程，设出P点坐标，代入AB得方程，求得若
PF1
•
PF2
的最小值，令(
PF1
•
PF2
)min＜0，结合椭圆的离心率的性质即可求得答案．
解答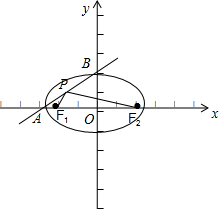：解：依题意，作图如下：
∵A（-a，0），B（0，b），F1（-c，0），F2（c，0），
∴直线AB的方程为：
x
-a
+
y
b
=1，整理得：bx-ay+ab=0，
设直线AB上的点P（x0，y0）
则bx0=ay0-ab，
∴x0=
a
b
y0-a，
∵
PF1
•
PF2
=（-c-x0，-y0）•（c-x0，-y0）=x02+y02-c2．
=(
a
b
y0-a)2+y02-c2，
令f（y0）=(
a
b
y0-a)2+y02-c2，
∵f′（y0）=2（
a
b
y0-a）×
a
b
+2y0，
∴由f′（y0）=0得：y0=
a2b
a2+b2
，于是x0=-
ab2
a2+b2
，
此时f（y0）取到最小值，
即(
PF1
•
PF2
)min=(
-ab2
a2+b2
)2+(
a2b
a2+b2
)2-c2，
∵(
PF1
•
PF2
)min＜0，
∴(
-ab2
a2+b2
)2+(
a2b
a2+b2
)2-c2＜0，
整理得：
a2b2
a2+b2
＜c2，又b2=a2-c2，e2=
c2
a2
，
∴e4-3e2+1＜0，
∴
3-
5
2
＜e2＜
3+
5
2
，又椭圆的离心率e∈（0，1），
∴
3-
5
2
＜e2＜1，
∵
3-
5
2
=
6-2
5
4
=(
5
-1
2
)2，
∴
5
-1
2
＜e＜1．
故选C．
点评：本题考查椭圆的性质，考查向量的数量积，考查直线的方程，着重考查函数的最值的求法，求得(
PF1
•
PF2
)min是关键，更是难点，属于难题．
练习册系列答案
相关题目
如图，已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0），焦点为F1、F2，双曲线G：x2-y2=m（m＞0）的顶点是该椭圆的焦点，设P是双曲线G上异于顶点的任一点，直线PF1、PF2与椭圆的交点分别为A、B和C、D，已知三角形ABF2的周长等于8
2
，椭圆四个顶点组成的菱形的面积为8
2
．
（1）求椭圆E与双曲线G的方程；
（2）设直线PF1、PF2的斜率分别为k1和k2，探求k1和k2的关系；
（3）是否存在常数λ，使得|AB|+|CD|=λ|AB|•|CD|恒成立？若存在，试求出λ的值；若不存在，请说明理由．
精英家教网
已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0），以F1（-c，0）为圆心，以a-c为半径作圆F1，过点B2（0，b）作圆F1的两条切线，设切点为M、N．
（1）若过两个切点M、N的直线恰好经过点B1（0，-b）时，求此椭圆的离心率；
（2）若直线MN的斜率为-1，且原点到直线MN的距离为4（
2
-1），求此时的椭圆方程；
（3）是否存在椭圆E，使得直线MN的斜率k在区间（-
2
2
，-
3
3
）内取值？若存在，求出椭圆E的离心率e的取值范围；若不存在，请说明理由．
已知椭圆E：
x2
a2
+
y2
3
=1（a＞
3
）的离心率e=
1
2
．直线x=t（t＞0）与曲线 E交于不同的两点M，N，以线段MN 为直径作圆 C，圆心为 C．
 （1）求椭圆E的方程；
 （2）若圆C与y轴相交于不同的两点A，B，求△ABC的面积的最大值．
（2012•佛山二模）已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的一个交点为F1(-
3
，0)，而且过点H(
3
，
1
2
)．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设椭圆E的上下顶点分别为A1，A2，P是椭圆上异于A1，A2的任一点，直线PA1，PA2分别交x轴于点N，M，若直线OT与过点M，N的圆G相切，切点为T．证明：线段OT的长为定值，并求出该定值．
已知椭圆E：
x2
a2
+y2=1（a＞1）的离心率e=
3
2
，直线x=2t（t＞0）与椭圆E交于不同的两点M、N，以线段MN为直径作圆C，圆心为C
（Ⅰ）求椭圆E的方程；
（Ⅱ）当圆C与y轴相切的时候，求t的值；
（Ⅲ）若O为坐标原点，求△OMN面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网