题目内容
8.若函数f(x)是幂函数,则f(1)=1,若满足f(4)=8f(2),则$f(\frac{1}{3})$=$\frac{1}{27}$.分析 设f(x)=xα,由幂函数的性质能求出结果.
解答 解:∵函数f(x)是幂函数,∴设f(x)=xα,
∴f(1)=1,
∵满足f(4)=8f(2),
∴4α=8×2α,解得α=3,
∴$f(\frac{1}{3})$=$(\frac{1}{3})^{3}$=$\frac{1}{27}$.
故答案为:1,$\frac{1}{27}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
16.命题“?x∈R,f(x)g(x)≠0”的否定是( )
| A. | ?x∈R,f(x)=0且g(x)=0 | B. | ?x∈R,f(x)=0或g(x)=0 | ||
| C. | ?x0∈R,f(x0)=0且g(x0)=0 | D. | ?x0∈R,f(x0)=0或g(x0)=0 |
17.某几何体的三视图及其尺寸如图所示,则该几何体的各侧面中,最大的侧面的面积为( )
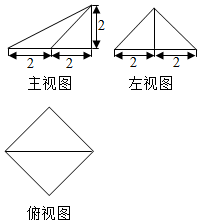

| A. | 4 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{6}$ |
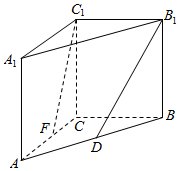 如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.