题目内容

若函数f（x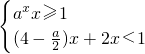）= $数学公式$ 是R上的单调递增函数，则实数a的取值范围是

A.
[4，8）
B.
（1，8）
C.
（4，8）
D.
（1，+∞）

C
分析：欲使函数f（x）在R上递增，须有f（x）在（-∞，1），[1，+∞）上递增，且满足（4- $\text{[math]}$ ）•1+2≤a¹，联立解不等式组即可．
解答：因为函数f（x）是R上的增函数，
所以有 $\text{[math]}$ ? $\text{[math]}$ ?4≤a＜8，
故选C．
点评：本题考查函数的单调性，考查学生对分段函数单调性质的理解，注意数形结合思想在分析本题中的应用．

练习册系列答案

小学数学口算题卡脱口而出系列答案

优秀生新口算题卡口算天天练系列答案

优秀生应用题卡口算天天练系列答案

黄冈新编口算题卡与应用题系列答案

浙江之星课时优化作业系列答案

学习宝典百分计划系列答案

完美大考卷系列答案

胜卷在握系列答案

优化学案系列答案

体验型学案系列答案

相关题目

（2012•贵阳模拟）若函数f（x）定义域为R，满足对任意x₁，x₂∈R，有f（x₁+x₂）≤f（x₁）+f（x₂），则称f（x）为“V形函数”；若函数g（x）定义域为R，g（x）恒大于0，且对任意x₁，x₂∈R，有lgg（x₁+x₂）≤lgg（x₁）+lgg（x₂），则称g（x）为“对数V形函数”．
（1）当f（x）=x²时，判断f（x）是否为V形函数，并说明理由；
（2）当g（x）=x²+2时，证明：g（x）是对数V形函数；
（3）若f（x）是V形函数，且满足对任意x∈R，有f（x）≥2，问f（x）是否为对数V形函数？证明你的结论．

若函数f（x）在定义域R上处处可导，则命题“f（x）的增函数”是命题“?x∈R，f′（x）＞0”成立的（　　）

A．充分不必要条件

B．必要不充分条件

C．充分必要条件

D．既非充分也非必要条件

函数f（x）定义域是R，有以下判断：
①若f（x）是偶函数，则f（-3）=f（3）；
②若f（-3）=-f（3），则f（x）是奇函数；
③若f（2＞f（-1），则f（x）是R上的增函数；
④若f（2）＞f（-1），则f（x）在R上不是减函数；
其中正确的判断是

．（填写序号）

（2012•上海模拟）若函数f（x）定义域为R，满足对任意x₁，x₂∈R，有f（x₁+x₂）≤f（x₁）+f（x₂），则称f（x）为“V形函数”．
（1）当f（x）=x²时，判断f（x）是否为V形函数，并说明理由；
（2）当f（x）=lg（x²+2）时，证明：f（x）是V形函数；
（3）当f（x）=lg（2^x+a）时，若f（x）为V形函数，求实数a的取值范围．

（2012•浦东新区二模）已知函数y=f（x），x∈D，如果对于定义域D内的任意实数x，对于给定的非零常数m，总存在非零常数T，恒有f（x+T）＞m•f（x）成立，则称函数f（x）是D上的m级类增周期函数，周期为T．若恒有f（x+T）=m•f（x）成立，则称函数f（x）是D上的m级类周期函数，周期为T．
（1）已知函数f（x）=-x²+ax是[3，+∞）上的周期为1的2级类增周期函数，求实数a的取值范围；
（2）已知 T=1，y=f（x）是[0，+∞）上m级类周期函数，且y=f（x）是[0，+∞）上的单调递增函数，当x∈[0，1）时，f（x）=2^x，求实数m的取值范围；
（3）下面两个问题可以任选一个问题作答，如果你选做了两个，我们将按照问题（Ⅰ）给你记分．
（Ⅰ）已知当x∈[0，4]时，函数f（x）=x²-4x，若f（x）是[0，+∞）上周期为4的m级类周期函数，且y=f（x）的值域为一个闭区间，求实数m的取值范围；
（Ⅱ）是否存在实数k，使函数f（x）=coskx是R上的周期为T的T级类周期函数，若存在，求出实数k和T的值，若不存在，说明理由．