题目内容
设函数 ,
,(1)当a=2,-2≤x≤2时,求f(x)的值域;
(2)若f(x)在x∈(-1,2)上是单调函数,求实数a的范围.
【答案】分析:(1)当a=2,-2≤x≤2时,f(x)=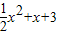 =
=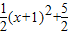 ,由此能求出f(x)的值域.
,由此能求出f(x)的值域.
(2)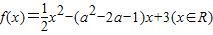 的对称轴方程是x=a2-2a-1,由f(x)在x∈(-1,2)上是单调函数,知a2-2a-1≥2或a2-2a-1≤-1,由此能求出实数a的范围.
的对称轴方程是x=a2-2a-1,由f(x)在x∈(-1,2)上是单调函数,知a2-2a-1≥2或a2-2a-1≤-1,由此能求出实数a的范围.
解答:解:(1)当a=2,-2≤x≤2时,
f(x)=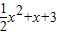 =
=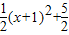 ,
,
∴当x=-1时,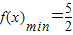 ,
,
当x=2时,f(x)max=7,
∴当a=2,-2≤x≤2时,f(x)的值域是[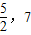 ].
].
(2)∵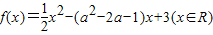 的对称轴方程是x=a2-2a-1,
的对称轴方程是x=a2-2a-1,
f(x)在x∈(-1,2)上是单调函数,
∴a2-2a-1≥2或a2-2a-1≤-1,
解得a≤-1,或0≤a≤2,或a≥3.
即实数a的范围是(-∞,-1]∪[0,2]∪[3,+∞).
点评:本题考查函数的值域和实数a的取值范围,是基础题.解题时要认真审题,注意二次函数的性质和配方法的灵活运用.
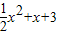 =
=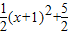 ,由此能求出f(x)的值域.
,由此能求出f(x)的值域.(2)
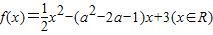 的对称轴方程是x=a2-2a-1,由f(x)在x∈(-1,2)上是单调函数,知a2-2a-1≥2或a2-2a-1≤-1,由此能求出实数a的范围.
的对称轴方程是x=a2-2a-1,由f(x)在x∈(-1,2)上是单调函数,知a2-2a-1≥2或a2-2a-1≤-1,由此能求出实数a的范围.解答:解:(1)当a=2,-2≤x≤2时,
f(x)=
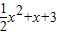 =
=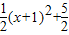 ,
,∴当x=-1时,
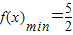 ,
,当x=2时,f(x)max=7,
∴当a=2,-2≤x≤2时,f(x)的值域是[
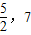 ].
].(2)∵
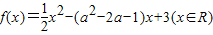 的对称轴方程是x=a2-2a-1,
的对称轴方程是x=a2-2a-1,f(x)在x∈(-1,2)上是单调函数,
∴a2-2a-1≥2或a2-2a-1≤-1,
解得a≤-1,或0≤a≤2,或a≥3.
即实数a的范围是(-∞,-1]∪[0,2]∪[3,+∞).
点评:本题考查函数的值域和实数a的取值范围,是基础题.解题时要认真审题,注意二次函数的性质和配方法的灵活运用.

练习册系列答案
相关题目
 。
。 的极值;
的极值; 2时,讨论函数
2时,讨论函数 成立,求
成立,求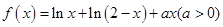 。
。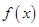 的单调区间。
的单调区间。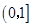 上的最大值为
上的最大值为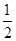 ,求a的值。
,求a的值。 。
。  的定义域。
的定义域。 。
。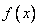 的单调区间。
的单调区间。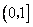 上的最大值为
上的最大值为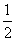 ,求a的值。
,求a的值。