题目内容
在直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.已知点A的极坐标为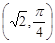 ,直线
,直线 的极坐标方程为
的极坐标方程为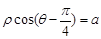 ,且点A在直线
,且点A在直线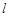 上。
上。
(Ⅰ)求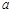 的值及直线
的值及直线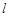 的直角坐标方程;
的直角坐标方程;
(Ⅱ)圆C的参数方程为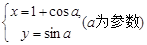 ,试判断直线l与圆C的位置关系.
,试判断直线l与圆C的位置关系.
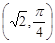 ,直线
,直线 的极坐标方程为
的极坐标方程为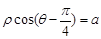 ,且点A在直线
,且点A在直线 上。
上。(Ⅰ)求
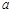 的值及直线
的值及直线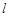 的直角坐标方程;
的直角坐标方程;(Ⅱ)圆C的参数方程为
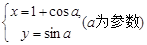 ,试判断直线l与圆C的位置关系.
,试判断直线l与圆C的位置关系.(Ⅰ) (Ⅱ)直线与圆相交
(Ⅱ)直线与圆相交
 (Ⅱ)直线与圆相交
(Ⅱ)直线与圆相交(Ⅰ)由点 在直线
在直线 上,可得
上,可得
所以直线 的方程可化为
的方程可化为
从而直线 的直角坐标方程为
的直角坐标方程为
(Ⅱ)由已知得圆 的直角坐标方程为
的直角坐标方程为
所以圆心为 ,半径
,半径
以为圆心到直线的距离 ,所以直线与圆相交
,所以直线与圆相交
坐标系与参数方程无非就是坐标系之间的互化,之后就变为简单的解析几何问题也属于必得分题目。
【考点定位】本题主要考查坐标间的互化以及圆的参数方程的基本内容,属于简单题。
 在直线
在直线 上,可得
上,可得
所以直线
 的方程可化为
的方程可化为
从而直线
 的直角坐标方程为
的直角坐标方程为
(Ⅱ)由已知得圆
 的直角坐标方程为
的直角坐标方程为
所以圆心为
 ,半径
,半径
以为圆心到直线的距离
 ,所以直线与圆相交
,所以直线与圆相交坐标系与参数方程无非就是坐标系之间的互化,之后就变为简单的解析几何问题也属于必得分题目。
【考点定位】本题主要考查坐标间的互化以及圆的参数方程的基本内容,属于简单题。

练习册系列答案
相关题目
 于F(不与B重合),直线
于F(不与B重合),直线 与
与
 ;(2)
;(2)
 的割线
的割线 交圆
交圆 、
、 两点,割线
两点,割线 经过圆心.已知
经过圆心.已知 ,
, ,
, .则圆
.则圆 .
.
 △
△ 中,斜边
中,斜边 ,直角边
,直角边 ,如果以
,如果以 为圆心的圆与
为圆心的圆与 相切于
相切于 ,则⊙
,则⊙
 ,此棱锥的侧棱与底面所成的角相等,则底面四边形的最小角是( ).
,此棱锥的侧棱与底面所成的角相等,则底面四边形的最小角是( ).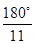
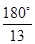
 是☉
是☉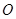 的内接四边形,
的内接四边形,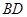 不经过点
不经过点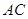 平分
平分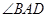 ,经过点
,经过点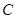 的直线分别交
的直线分别交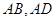 的延长线于点
的延长线于点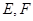 ,且
,且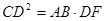 ,证明:
,证明: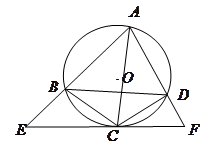
 ∽
∽ ;
; 是☉
是☉ ,则线段AC的长度为 .
,则线段AC的长度为 .
 ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长.
 中,
中,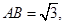
 ,
,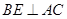 ,垂足为
,垂足为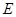 ,则
,则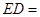 .
.