Question

已知△ABC的外接圆中，D、E分别为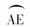与的中点，弦DE交AB、AC于F、G.求证：AF=AG.

图2-1-13

Answer 1

思路分析：可以通过等角对等边来证明此题，即证明∠AFE=∠AGF，将∠AFE、∠AGF分别看作△FBE与△DGC的外角，利用已知中D、E为、的中点可以证明角相等.

证明：连结BE、CD,∠AFE=∠1+∠2,

又∠1+∠2(+),

∴∠AFE(+).

∴∠AGD(+)∠3+∠4.

∵D、E为、中点，∴=，=.

∴∠AFE=∠AGD.∴AF=AG.

    深化升华

角的度数与弧的度数相等时，常采用如下记号表示：∠α，即在等号的上方加上字母m.