题目内容
已知a,b是不相等的正数,在a,b之间分别插入m个正数a1,a2, ,am和正数b1,b2, ,
bm,使a,a1,a2, ,am,b是等差数列,a,b1,b2, ,bm,b是等比数列.
(1)若m=5, =
= ,求
,求 的值;
的值;
(2)若b=λa(λ∈N*,λ≥2),如果存在n (n∈N*,6≤n≤m)使得an-5=bn,求λ的最小值及此时m的值;
(3)求证:an>bn(n∈N*,n≤m).
bm,使a,a1,a2, ,am,b是等差数列,a,b1,b2, ,bm,b是等比数列.
(1)若m=5,
 =
= ,求
,求 的值;
的值;(2)若b=λa(λ∈N*,λ≥2),如果存在n (n∈N*,6≤n≤m)使得an-5=bn,求λ的最小值及此时m的值;
(3)求证:an>bn(n∈N*,n≤m).
(1)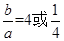 ;(2)
;(2) 最小值为4,此时
最小值为4,此时 为29;(3)详见解析
为29;(3)详见解析
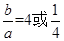 ;(2)
;(2) 最小值为4,此时
最小值为4,此时 为29;(3)详见解析
为29;(3)详见解析试题分析:(1)根据题意m=5时,共有7项,设等差数列的公差为
 ,等比数列的公比为
,等比数列的公比为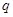 ,则
,则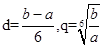 ,表示出
,表示出 ,又由
,又由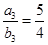 ,可得到
,可得到 ,解得
,解得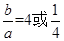 ;(2)由条件得
;(2)由条件得 ,即
,即 ,从而得
,从而得 ,又由于
,又由于 ,即
,即 ,从而得
,从而得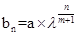 ,又题中有
,又题中有 ,可得
,可得 , 化简消去a得:
, 化简消去a得: ,观察此式结构特征:
,观察此式结构特征: ,则要求
,则要求 为有理数.即
为有理数.即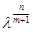 必须为有理数,而
必须为有理数,而 ,可将
,可将 用数字代入检验: 若
用数字代入检验: 若 ,则
,则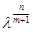 为无理数,不满足条件; 同理,
为无理数,不满足条件; 同理,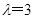 不满足条件; 当
不满足条件; 当 时,
时, .要使
.要使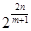 为有理数,则
为有理数,则 必须为整数,要满足
必须为整数,要满足  ,可解得
,可解得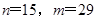 ;(3)可假设
;(3)可假设 ,
, 为数列
为数列 的前
的前 项的和,我们易先证:若
项的和,我们易先证:若 为递增数列,则
为递增数列,则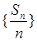 为递增数列;同理可证,若
为递增数列;同理可证,若 为递减数列,则
为递减数列,则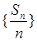 为递减数列;由于a和b的大小关系不确定,故要对其分类讨论:①当
为递减数列;由于a和b的大小关系不确定,故要对其分类讨论:①当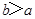 时,
时, .当
.当 时,
时,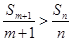 .即
.即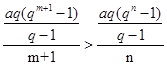 ,即
,即 .因为
.因为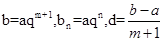 ,所以
,所以 ,即
,即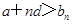 ,即
,即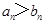 ;②当
;②当 时,同理可求得
时,同理可求得 .
.试题解析:(1)设等差数列的公差为
 ,等比数列的公比为
,等比数列的公比为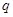 ,
,则
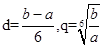 .
. . 2分
. 2分因为
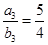 ,所以
,所以 ,解得
,解得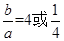 . 4分
. 4分(2)因为
 ,所以
,所以 ,从而得
,从而得 .
.因为
 ,所以
,所以 ,从而得
,从而得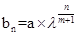 .
.因为
 ,所以
,所以 .
.因为
 ,所以
,所以 (*). 6分
(*). 6分因为
 ,所以
,所以 为有理数.
为有理数.要使(*)成立,则
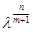 必须为有理数.
必须为有理数.因为
 ,所以
,所以 .
.若
 ,则
,则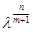 为无理数,不满足条件.
为无理数,不满足条件.同理,
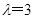 不满足条件. 8分
不满足条件. 8分当
 时,
时, .要使
.要使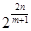 为有理数,则
为有理数,则 必须为整数.
必须为整数.又因为
 ,所以仅有
,所以仅有 满足条件.
满足条件.所以
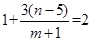 ,从而解得
,从而解得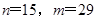 .
.综上,
 最小值为4,此时
最小值为4,此时 为29. 10分
为29. 10分(3)设
 ,
, 为数列
为数列 的前
的前 项的和.
项的和.先证:若
 为递增数列,则
为递增数列,则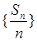 为递增数列.
为递增数列.证明:当
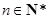 时,
时, .
. 因为
 ,所以
,所以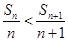 ,即数列
,即数列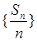 为递增数列.
为递增数列. 同理可证,若
 为递减数列,则
为递减数列,则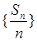 为递减数列. 12分
为递减数列. 12分①当
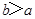 时,
时, .当
.当 时,
时,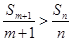 .
.即
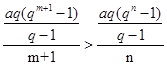 ,即
,即 .
. 因为
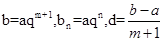 ,
,所以
 ,即
,即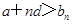 ,即
,即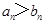 .
. ②当
 时,
时, ,当
,当 时,
时, .
.即
 .
.因为
 ,所以
,所以 .以下同①.
.以下同①.综上,
 . 16分
. 16分
练习册系列答案
相关题目
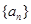 的首项
的首项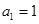 ,公差
,公差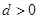 ,且第
,且第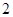 项、第
项、第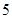 项、第
项、第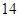 项分别是等比数列
项分别是等比数列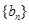 的第
的第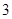 项、第
项、第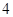 项.
项.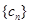 对任意
对任意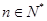 ,均有
,均有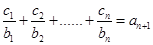 成立.
成立.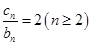 ; ②求
; ②求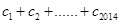 .
. 是正数组成的数列,其前
是正数组成的数列,其前 项和为
项和为 ,且对所有的正整数
,且对所有的正整数 与2的等差中项等于
与2的等差中项等于 ,定义
,定义 .
. ,则
,则 ;
; ,则
,则 的取值范围是 .
的取值范围是 . 中,
中, ,则数列
,则数列 =______________.
=______________.
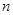 层
层 的点数为___________个;
的点数为___________个; 为等比数列,
为等比数列, 存在等比中项
存在等比中项 ,,则
,,则
 为等差数列,
为等差数列, 为等比数列,
为等比数列, ,则
,则 ( )
( )


