题目内容
已知等差数列{an}中,a3=-11,a1+a6=-20
(1)求数列{an}的通项公式
(2)求数列{an}的前n项和Sn,并判断当n取何值时,Sn有最小值.
(1)求数列{an}的通项公式
(2)求数列{an}的前n项和Sn,并判断当n取何值时,Sn有最小值.
考点:等差数列的前n项和,等差数列的通项公式
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列通项公式列出方程组,求出首项与公差,由此能求出数列{an}的通项公式.
(2)求出等差数列的前n项和,利用配方法能求出当n取8时,Sn有最小值.
(2)求出等差数列的前n项和,利用配方法能求出当n取8时,Sn有最小值.
解答:
解:(1)∵等差数列{an}中,a3=-11,a1+a6=-20,
∴
,解得a1=-15,d=2,
∴an=-15+(n-1)×2=2n-17.
(2)Sn=-15n+
×2
=n2-16n
=(n-8)2-64,
∴n=8时,Sn有最小值得.
∴
|
∴an=-15+(n-1)×2=2n-17.
(2)Sn=-15n+
| n(n-1) |
| 2 |
=n2-16n
=(n-8)2-64,
∴n=8时,Sn有最小值得.
点评:本题考查等差数列的通项公式的求法,考查当n取何值时,Sn有最小值的求法,是基础题,解题时要认真审题,注意配方法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,a=1,B=45°,S△ABC=2,则△ABC的外接圆半径为( )
A、2
| ||||
B、3
| ||||
C、
| ||||
D、
|
给出下面四个命题,其中正确的一个是( )
A、回归直线
| ||||||
| B、在线性回归模型中,相关指数R2=0.64,说明预报变量对解释变量个贡献率是64% | ||||||
| C、相关指数R2用来刻画回归效果,R2越小,则残差平方的和越大,模型的拟合效果越好 | ||||||
| D、随机误差e是引起预报值与真实值之间存在误差的原因之一 |

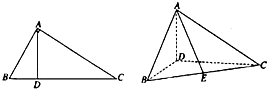 如图,在△ABC中,AB⊥AC,AD⊥BC,∠ABC=
如图,在△ABC中,AB⊥AC,AD⊥BC,∠ABC= 已知椭圆C方程:
已知椭圆C方程: