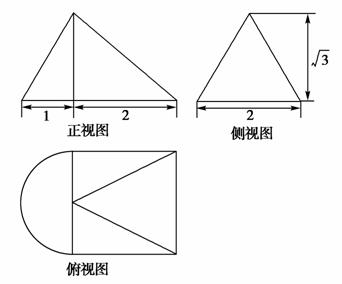
题目内容
已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为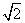 ,且过点(4,-
,且过点(4,- ).
).
(1)求双曲线的方程;
(2)若点M(3,m)在双曲线上,求证: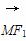 ·
·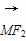 =0;
=0;
(3)在(2)的条件下,求△F1MF2的面积.
(1)∵e=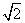 ,
,
∴可设双曲线方程为x2-y2=λ(λ≠0),
∵双曲线过点(4,- ),∴16-10=λ,即λ=6,
),∴16-10=λ,即λ=6,
∴双曲线方程为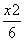 -
-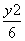 =1.
=1.
(2)证明:法1:由(1)可知,双曲线中a=b=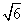 ,
,
∴c=2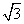 ,
,
∴F1(-2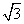 ,0),F2(2
,0),F2(2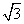 ,0),
,0),
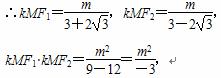 ∵点M(3,m)在双曲线上,∴m2=3,
∵点M(3,m)在双曲线上,∴m2=3,
∴kMF1·kMF2=-1,∴MF1⊥MF2,即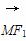 ·
·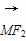 =0.
=0.
法2:∵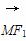 =(-2
=(-2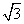 -3,-m),
-3,-m),
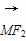 =(2
=(2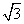 -3,-m),
-3,-m),
∴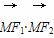 =(-2
=(-2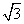 -3)×(2
-3)×(2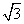 -3)+m2=-3+m2,
-3)+m2=-3+m2,
∵点M在双曲线上,
∴9-m2=6,即m2-3=0,∴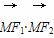 =0.
=0.
(3)∵△F1MF2的底边长|F1F2|=4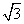 ,△F1MF2的高h=|m|=
,△F1MF2的高h=|m|=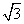 ,
,
∴S△F1MF2=6.

练习册系列答案
相关题目
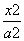 +
+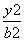 =1(a>0,b>0)的左焦点,若椭圆上存在点P,使得直线PF与圆x2+y2=b2相切,当直线PF的倾斜角为
=1(a>0,b>0)的左焦点,若椭圆上存在点P,使得直线PF与圆x2+y2=b2相切,当直线PF的倾斜角为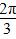 时,此椭圆的离心率是________.
时,此椭圆的离心率是________.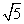 ,则它的渐近线方程为( )
,则它的渐近线方程为( )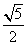 x
x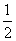 x D.y=±
x D.y=±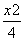 -
-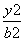 =1(b>0)的左焦点F1作⊙O2:x2+y2=4的两条切线,记切点为A,B,双曲线的左顶点为C,若∠ACB=120°,则双曲线的离心率为( )
=1(b>0)的左焦点F1作⊙O2:x2+y2=4的两条切线,记切点为A,B,双曲线的左顶点为C,若∠ACB=120°,则双曲线的离心率为( )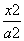 -y2=1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则
-y2=1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则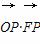 的取值范围为( )
的取值范围为( )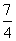 ,+∞) D.[
,+∞) D.[ x2上的动点,点P在x轴上的射影为M,点A的坐标是(2,0),则|PA|+|PM|的最小值是________.
x2上的动点,点P在x轴上的射影为M,点A的坐标是(2,0),则|PA|+|PM|的最小值是________.