题目内容
若Fl、F2为双曲线C:
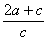
(1)求双曲线C的离心率及其方程;
(2)设双曲线C的虚轴端点为B1、B2(B1在y轴的正半轴上),点A、B在双曲线上,且![]() 当
当![]() =0时,求直线AB的方程.
=0时,求直线AB的方程.
解:(1)∵
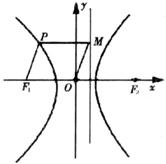
∴四边形OF1PM为菱形.
设F1(-c,0),则|PF1|=|PM|=c
由双曲线第一定义,得|PF2|=2a+c
由双曲线第二定义,得![]() =e,即
=e,即![]() =e
=e
整理,得e2-e-2=0 解得e=2(e=-1舍去)
此时C的方程为![]() =1,将N(2,
=1,将N(2,![]() )代入得,a2=3
)代入得,a2=3
∴双曲线方程为![]() =1
=1
(2)依题意B1(0,3),B2(0,-3)
∵![]()
∴ A、B、B2三点共线,设其方程为y=kx-3.
由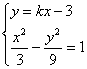 得(3-k2)x2+6kx-18=0.(*),
得(3-k2)x2+6kx-18=0.(*),
设A(x1,y1),B(x2,y2),
∵k≠±![]() ∴x1+x2=
∴x1+x2=![]() ,x1x2=
,x1x2=![]()
y1+y2=k(x1+x2)-6=![]() ,
,
yly2=k2x1x2-3k(x1+x2)+9=9
∵![]() =0 ∴(xl,y1-3)·(x2,y2-3)=0
=0 ∴(xl,y1-3)·(x2,y2-3)=0
∴x1x2+y1y2-3(y1+y2)+9=0
∴![]() +9-3·
+9-3·![]() +9=0,解得k=±
+9=0,解得k=±![]()
此时方程(*)中,△>0.故所求直线方程为y=±![]() x-3
x-3

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目