题目内容
如果函数y=f(x)图象上任意一点的坐标(x,y)都满足方程lg(x+y)=lgx+lgy,那么y=f(x)在[2,4]上的最小值是________.

由lg(x+y)=lgx+lgy,得 ,由x+y=xy得y=f(x)=
,由x+y=xy得y=f(x)= =
= =1+
=1+ (x≠1).则函数f(x)在(1,+∞)上单调递减,所以y=f(x)在[2,4]上的最小值是f(4)=1+
(x≠1).则函数f(x)在(1,+∞)上单调递减,所以y=f(x)在[2,4]上的最小值是f(4)=1+ =
= .
.
 ,由x+y=xy得y=f(x)=
,由x+y=xy得y=f(x)= =
= =1+
=1+ (x≠1).则函数f(x)在(1,+∞)上单调递减,所以y=f(x)在[2,4]上的最小值是f(4)=1+
(x≠1).则函数f(x)在(1,+∞)上单调递减,所以y=f(x)在[2,4]上的最小值是f(4)=1+ =
= .
.
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 上的三个函数
上的三个函数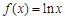 ,
, ,
, ,且
,且 在
在 处取得极值.
处取得极值.

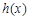 的单调区间.
的单调区间.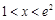 时,恒有
时,恒有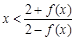 成立.
成立.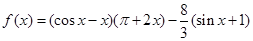 ,
,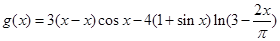 .
.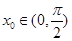 ,使
,使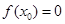 ;
;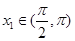 ,使
,使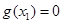 ,且对(1)中的
,且对(1)中的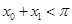 .
. ,在使
,在使 的下确界为 .
的下确界为 . )
)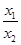 )=f(x1)-f(x2),且当x>1时,f(x)<0.
)=f(x1)-f(x2),且当x>1时,f(x)<0. 是奇函数.
是奇函数.

