题目内容
【题目】已知![]() ,函数
,函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求a的取值范围;
上单调递增,求a的取值范围;
(2)用反证法证明:函数![]() 不可能为
不可能为![]() 上的单调函数.
上的单调函数.
【答案】(1)![]() .(2)证明见解析
.(2)证明见解析
【解析】
(1)函数![]() 在
在![]() 上单调递增,说明
上单调递增,说明![]() ,对于
,对于![]() 都成立,得到
都成立,得到![]() ,令
,令![]() ,则
,则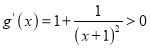 ,转化求解即可;
,转化求解即可;
(2)证明:假设![]() 为
为![]() 上单调函数,则为
上单调函数,则为![]() 上单调递增函数或
上单调递增函数或![]() 上单调递减函数,
上单调递减函数,
①若函数![]() 为
为![]() 上单调递增函数,则
上单调递增函数,则![]() ,对于
,对于![]() 都成立,推出
都成立,推出![]() 不可能为
不可能为![]() 上的单调增函数,②若函数
上的单调增函数,②若函数![]() 为
为![]() 上单调递减函数,则
上单调递减函数,则![]() ,对于
,对于![]() 都成立,推出
都成立,推出![]() 不能为
不能为![]() 上的单调递减函数,说明函数
上的单调递减函数,说明函数![]() 不可能为
不可能为![]() 上的单调函数.
上的单调函数.
(1)函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,对于
,对于![]() 都成立,
都成立,
即![]() ,对于
,对于![]() 都成立,
都成立,
故有![]() ,
,
令![]() ,则
,则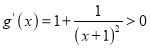 ,
,
故![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
∴a的取值范围是![]() ;
;
(2)假设![]() 为R上单调函数,则为R上单调递增函数或R上单调递减函数,
为R上单调函数,则为R上单调递增函数或R上单调递减函数,
①若函数![]() 为R上单调递增函数,则
为R上单调递增函数,则![]() ,对于
,对于![]() 都成立,
都成立,
即![]() 恒成立.
恒成立.
由![]() ,
,![]() 对于
对于![]() 都恒成立,
都恒成立,
由![]() 的开口向上的抛物线,
的开口向上的抛物线,
则![]() ,不可能恒成立,
,不可能恒成立,
所以![]() 不可能为R上的单调增函数;
不可能为R上的单调增函数;
②若函数![]() 为R上单调递减函数,则
为R上单调递减函数,则![]() ,对于
,对于![]() 都成立,
都成立,
即![]() 恒成立,
恒成立,
由![]() ,
,![]() 对于
对于![]() 都恒成立,
都恒成立,
故由![]() ,整理得:
,整理得:![]() ,显然不成立,
,显然不成立,
所以,![]() 不能为R上的单调递减函数,
不能为R上的单调递减函数,
综上,可知函数![]() 不可能为R上的单调函数.
不可能为R上的单调函数.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除
的包裹,除![]() 收费10元之外,超过
收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() 时按
时按![]() 计算)需再收5元.公司从承揽过的包裹中,随机抽取100件,其重量统计如下:
计算)需再收5元.公司从承揽过的包裹中,随机抽取100件,其重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 | 43 | 30 | 15 | 8 | 4 |
公司又随机抽取了60天的揽件数,得到频数分布表如下:
揽件数 |
|
|
|
|
|
天数 | 6 | 6 | 30 | 12 | 6 |
以记录的60天的揽件数的频率作为各揽件数发生的概率
(1)计算该公司3天中恰有2天揽件数在![]() 的概率;
的概率;
(2)估计该公司对每件包裹收取的快递费的平均值;
(3)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用做其他费用,目前前台有工作人员3人,每人每天揽件不超过150件,每人每天工资100元,公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润有利?
(注:同一组中的揽件数以这组数据所在区间中点值作代表)