题目内容
设函数 则满足|f(x)|<2的x的取值范围是( )
则满足|f(x)|<2的x的取值范围是( )A.(-∞,-1)∪[0,3)
B.(-∞,-1]∪[0,3]
C.(-∞,-1)(0,3)
D.(-∞,3)
【答案】分析:根据题意,原不等式可转化为:当x<0时,f(x)=| |=
|= <2,当x≥0,-2<log2(x+1)<2,求解不等式即可
<2,当x≥0,-2<log2(x+1)<2,求解不等式即可
解答:解:∵|f(x)|<2
当x<0时,f(x)=| |=
|= <2,解可得x<-1
<2,解可得x<-1
当x≥0,-2<log2(x+1)<2,解可得
∴0≤x<3
综上可得,x的取值范围是(-∞,-1)∪[0,3)
故选A
点评:本题主要考查了分段函数的应用及指数、对数不等式的求解,属于基础试题
 |=
|= <2,当x≥0,-2<log2(x+1)<2,求解不等式即可
<2,当x≥0,-2<log2(x+1)<2,求解不等式即可解答:解:∵|f(x)|<2
当x<0时,f(x)=|
 |=
|= <2,解可得x<-1
<2,解可得x<-1当x≥0,-2<log2(x+1)<2,解可得

∴0≤x<3
综上可得,x的取值范围是(-∞,-1)∪[0,3)
故选A
点评:本题主要考查了分段函数的应用及指数、对数不等式的求解,属于基础试题

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
设min{p,q}表示p,q两者中的较小者,若函数f(x)=min{3-x,log2x},则满足f(x)<
的x的集合为( )
| 1 |
| 2 |
A、(0,
| ||||
| B、(0,+∞) | ||||
C、(0,2)∪(
| ||||
D、(
|
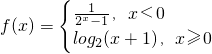 则满足|f(x)|<2的x的取值范围是
则满足|f(x)|<2的x的取值范围是