题目内容
过直线y=x上的一点P作圆(x-5)2+(y-1)2=2的两条切线l1,l2,A,B为切点,当直线l1,l2关于直线y=x对称时,则∠APB=
- A.30°
- B.45°
- C.60°
- D.90°
C
分析:判断圆心与直线的关系,在直线上求出特殊点,P的方程,利用切线长、半径以及该点与圆形连线构成直角三角形,求出∠APB的值.
解答:显然圆心(5,1)不在直线y=x上.
由对称性可知,只有直线y=x上的特殊点,这个点与圆心连线垂直于直线y=x,从这点做切线才能关于直线y=x对称.
所以该点与圆形连线所在的直线方程为:y-5=-(x-1)即 y=6-x
与 y=x联立可求出该点坐标为(3,3),
所以该点到圆心的距离为((5-3)2+(1-3)2=2
切线长、半径以及该点与圆形连线构成直角三角形,又知圆的半径为 .
.
所以夹角的一半的正弦值为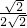 =
=
所以夹角∠APB=60°
故选C.
点评:本题是中档题,考查直线与圆的位置关系,直线与圆相切的关系的应用,考查计算能力,常考题型.
分析:判断圆心与直线的关系,在直线上求出特殊点,P的方程,利用切线长、半径以及该点与圆形连线构成直角三角形,求出∠APB的值.
解答:显然圆心(5,1)不在直线y=x上.
由对称性可知,只有直线y=x上的特殊点,这个点与圆心连线垂直于直线y=x,从这点做切线才能关于直线y=x对称.
所以该点与圆形连线所在的直线方程为:y-5=-(x-1)即 y=6-x
与 y=x联立可求出该点坐标为(3,3),
所以该点到圆心的距离为((5-3)2+(1-3)2=2

切线长、半径以及该点与圆形连线构成直角三角形,又知圆的半径为
 .
.所以夹角的一半的正弦值为
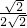 =
=
所以夹角∠APB=60°
故选C.
点评:本题是中档题,考查直线与圆的位置关系,直线与圆相切的关系的应用,考查计算能力,常考题型.

练习册系列答案
相关题目
过直线y=x上的一点作圆x2+(y-4)2=2的两条切线L1、L2,当L1与L2关于y=x对称时,L1与L2的夹角为( )
| A、30° | B、45° | C、60° | D、90° |