题目内容
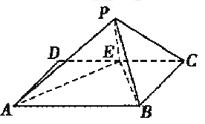
【题目】如图所示，
是半圆
的直径，
垂直于半圆所在的平面，点
是圆周上不同于
的任意一点，
分别为
的中点，则下列结论正确的是( )
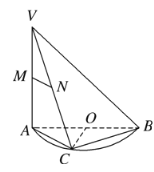
A.
B.平面
平面
C.
与
所成的角为45°D.
平面
【答案】B
【解析】
对每一个选项逐一分析判断得解.
A.
，
分别为
，
的中点，
，又
，
与
所成的角为
，故
不正确；
，
，
不成立，故A不正确．
B. 
是
的直径，点是圆周上不同于
，
的任意一点，
，
垂直所在的平面，
所在的平面，
，
又
，
平面
，
又
平面
，
平面
平面，故B正确；
C. 是的直径，点是圆周上不同于，的任意一点，
，又、、、
共面，
与
不垂直，
平面不成立，故不正确；
，分别为，的中点，
，又，与所成的角为，故不正确；
D. 是的直径，点是圆周上不同于，的任意一点，
，又、、、共面，与不垂直，
平面不成立，故D不正确.
故选:B.
练习册系列答案
阅读快车系列答案
相关题目
