题目内容
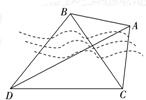 如图,为测量河对岸A、B两点的距离,在河的这边取C、D两点观察、测得CD=
如图,为测量河对岸A、B两点的距离,在河的这边取C、D两点观察、测得CD=| 3 |
分析:根据题中条件先分别求出∠DAC,∠DBC.在△ADC中由正弦定理求得AD,在△CDB中由正弦定理求得DB,最后△ADB中由余弦定理求得AB
解答:解:∠DAC=180°-∠ADC-∠DCB-∠ACB=30°,∠DBC=180°-∠DCB-∠ADC-∠ADB=60°
在△ADC中由正弦定理得:
=
∴AD=sin(∠DCB+∠ACB)
=3
在△CDB中由正弦定理得:
=
∴DB=
sin∠DCB=
在△ADB中由余弦定理得:AB2=DB2+AD2-2DB•ABcos∠ADB=2+9-2×
×3×
=5
∴AB=
km
答:A、B两点间的距离为
km
在△ADC中由正弦定理得:
| DC |
| sin∠DAC |
| AD |
| sin(∠DCB+∠ACB) |
∴AD=sin(∠DCB+∠ACB)
| DC |
| sin∠DAC |
在△CDB中由正弦定理得:
| CD |
| sin∠DBC |
| DB |
| sin∠DCB |
∴DB=
| CD |
| sin∠DBC |
| 2 |
在△ADB中由余弦定理得:AB2=DB2+AD2-2DB•ABcos∠ADB=2+9-2×
| 2 |
| ||
| 2 |
∴AB=
| 5 |
答:A、B两点间的距离为
| 5 |
点评:本题主要考查正弦定理和余弦定理在实际中的应用.由于图象中三角形比较多,应分清在哪个三角形中利用正弦定理和余弦定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
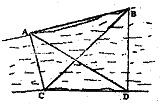 如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40米的C、D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,则AB的距离为( )
如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40米的C、D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,则AB的距离为( )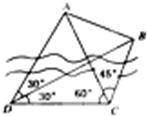 如图,为了测量河对岸A,B两点间的距离,在河的这边测得CD=
如图,为了测量河对岸A,B两点间的距离,在河的这边测得CD=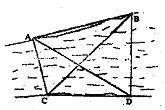
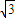 km,∠ADB=45°,∠ADC=30°,∠ACB=75°,∠DCB=45°,(A、B、C、D在同一平面内),求A、B两点间的距离.
km,∠ADB=45°,∠ADC=30°,∠ACB=75°,∠DCB=45°,(A、B、C、D在同一平面内),求A、B两点间的距离.