题目内容
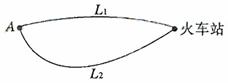
如图,A地到火车站共有两条路径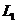 和
和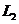 ,现随机抽取100位从A地到达火车站的人进行调查,调查结果如下:
,现随机抽取100位从A地到达火车站的人进行调查,调查结果如下:
|
所用时间(分钟) |
10 |
20 |
30 |
40 |
50 |
|
选择 |
6 |
12 |
18 |
12 |
12 |
|
选择 |
0 |
4 |
16 |
16 |
4 |
(1)试估计40分钟内不能赶到火车站的概率;
(2 )分别求通过路径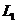 和
和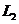 所用时间落在上表中各时间段内的频率;
所用时间落在上表中各时间段内的频率;
(3)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
【分析】(1)读懂数表,确定不能赶到火车站的人数所在的区间,用相应的频率作为所求概率的估计值;(2)根据频率的计算公式计算;(3)计算选择不同的路径,在允许的时间内赶往火车站的概率,通过比较概率的大小确定选择的最佳路径.
【解】(1)由已知共调查了100人,其中40分钟内不能赶到火车站的有12+12+16+4=44人,
 用频率估计相应的概率为0.44.
用频率估计相应的概率为0.44.
(2 )选择 的有60人,选择
的有60人,选择 的有40人,
的有40人,
故由调查结果得频率为:
|
所用时间(分钟) |
10 |
20 |
30 |
40 |
50 |
|
选择 |
0.1 |
0.2 |
0.3 |
0.2 |
0.2 |
|
选择 |
0 |
0.1 |
0.4 |
0.4 |
0.1 |
(3)用 ,
, 分别表示甲选择
分别表示甲选择 和
和 时,在40分钟内赶到火车站;用
时,在40分钟内赶到火车站;用 ,
, 分别表示乙选择
分别表示乙选择 和
和 时,在50分钟内赶到火车站.
时,在50分钟内赶到火车站.
由(2)知P(A1) =0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5, P(A1) P(A2),
P(A2),
 甲应选择路径
甲应选择路径 ;
;
P(B1) =0.1+0.2+0.3+0.2=0.8,P(B2)=0.1+0.4+0.4=0.9,P(B2)>P(B1),
∴ 乙应选择路径L2.

| 所用时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| L1的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
| L2的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
(Ⅰ)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(Ⅱ)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求X的分布列和数学期望.
本小题满分13分)
如图,A地到火车站共有两条路径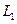 和
和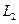 ,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
| 时间(分钟) | 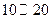 | 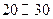 | 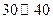 |  | 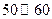 |
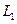 的频率 的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
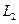 的频率 的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
(Ⅰ)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(Ⅱ)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求X的分布列和数学期望。
如图,A地到火车站共有两条路径L1,L2,现随机抽取100位从A地到火车站的人进行调查,结果如下:
|
所用时间(min) |
10~20 |
20~30 |
30~40 |
40~50 |
50~60 |
|
选择L1人数 |
6 |
12 |
18 |
12 |
12 |
|
选择L2人数 |
0 |
4 |
16 |
16 |
4 |
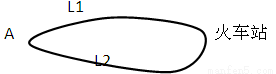
(1)试估计40 min内不能赶到火车站的概率
(2)现甲有40 min时间赶往火车站,为尽最大可能在允许的时间内赶到火车站,试通过计算说明,他如何选路径
 20
20 20
20 20、如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
20、如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下: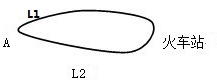 如图,A地到火车站共有两条路径L1,L2,现随机抽取100位从A地到火车站的人进行调查,结果如下:
如图,A地到火车站共有两条路径L1,L2,现随机抽取100位从A地到火车站的人进行调查,结果如下: