题目内容

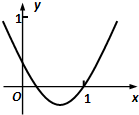
如图是函数f（x）=x2+ax+b的部分图象，则函数g（x）=lnx+f′（x）的零点所在的区间是（　　）
A．（
1
4
，
1
2
）		B．（1，2）C．（
1
2
，1）		D．（2，3）
精英家教网
由函数f（x）=x2+ax+b的部分图象得0＜b＜1，f（1）=0，从而-2＜a＜-1，
而g（x）=lnx+2x+a在定义域内单调递增，
g（
1
2
）=ln
1
2
+1+a＜0，
g（1）=ln1+2+a=2+a＞0，
∴函数g（x）=lnx+f′（x）的零点所在的区间是（
1
2
，1）；
故选C．
练习册系列答案
相关题目
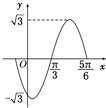精英家教网如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜π），x∈R的部分图象，则下列命题中，正确命题的序号为
 
．
①函数f（x）的最小正周期为
π
2
；
②函数f（x）的振幅为2
3
；
③函数f（x）的一条对称轴方程为x=
7π
12
；
④函数f（x）的单调递增区间为[
π
12
，
7π
12
]；
⑤函数的解析式为f（x）=
3
sin（2x-
2π
3
）．
已知如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的部分图象
（1）求函数解析式，写出f（x）的单调减区间
（2）当x∈[
π
12
，
π
2
]，求f（x）的值域．
（3）当x∈R时，求使f（x）≥1 成立的x 的取值集合．
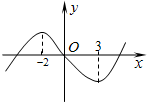如图是函数f（x）=x3+bx2+cx+d图象，则函数y=x2+2bx+c的单调递增区间为（　　）
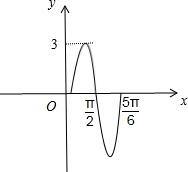如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤
π
2
）的图象的一部分，则其解析式f（x）=
3sin（3x-
π
2
）
3sin（3x-
π
2
）
．
（2013•温州二模）若如图是函数f（x）=sin2x和函数g（x）的部分图象，则函数g（x）的解析式可能是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网