Question

（2005•海淀区二模）将函数f(x)=

4-x2 (-2≤x≤0) 2-x(0＜x≤2)

的图象绕x轴旋转一周所得几何体的表面积为

(8+4

2

)π

；其体积为

8π

．

Answer 1

分析：作出函数f（x）的图象，得到图象是由圆心角为直角的扇形AOB和线段BC构成，从而得到f（x）的图象绕x轴旋转一周，所得几何体是由半球和圆锥组合而成的几何体．由此结合题中的数据加以计算，可得本题答案．

解答：解：根据题意，作出图象，可得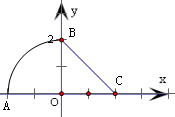
函数f(x)=

4-x2 (-2≤x≤0) 2-x(0＜x≤2)

的图象是由圆心角为直角的扇形AOB
和线段BC构成，其中A（-2，0），B（0，2），C（2，0）
因此，该图象绕x轴旋转一周，所得几何体是由半球和圆锥组合而成
半球的半径R=2，圆锥的底面半径为2，高等于2且母线长等于2

2

∵S_半球=

1

2

×4π×2²=8π，S_圆锥侧=π×2×2

2

=4

2

π
∴所得几何体的表面积为S=S_半球+S_圆锥侧=(8+4

2

)π
又∵V_半球=

1

2

×

4π

3

×23=

16π

3

，V_圆锥=

1

3

×π×2²×2=

8π

3

∴所得几何体的体积为V=V_半球+V_圆锥=

16π

3

+

8π

3

=8π
故答案为：(8+4

2

)π；8π

点评：本题将分段函数的图象绕x轴旋转一周，求旋转成的几何体的表面积和体积．着重考查了球和圆锥的表面积公式、体积公式和函数图象的作法等知识，属于中档题．