Question

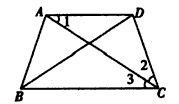
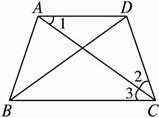
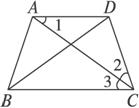
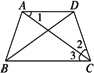
梯形的两腰和一底如果相等，它的对角形必平分另一底上的两个角．已知在梯形ABCD中(如图)，AB＝DC＝AD，AC和BD是它的对角线．求证：AC平分∠BCD，DB平分∠CBA．

Answer 1

答案：
解析：

证明：(1)等腰三角形两底角相等(大前提)，△DAC是等腰三角形，DA、DC是两腰(小前提)，∠1＝∠2(结论)． 　　(2)两条平行线被第三条直线截出的内错角相等(大前提)，∠1和∠3是平行线AD、BC被AC截出的内错角(小前提)，∠1＝∠3(结论)． 　　(3)等于同一个量的两个量相等(大前提)，∠2和∠3都等于∠1(小前提)，∠2＝∠3(结论)，即AC平分∠BCD． 　　(4)同理，DB平分∠CBA．