题目内容
20.设函数f(x)=-x2+ax+2(x2-x)lnx.(Ⅰ)当a=2时,求f(x)的单调区间;
(Ⅱ)若x∈(0,+∞)时,f(x)+x2>0恒成立,求整数a的最小值.
分析 (Ⅰ)求出函数f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)问题转化为a>-2(x-1)lnx恒成立,令g(x)=-2(x-1)lnx,根据函数的单调性求出a的最小值即可.
解答 解:(Ⅰ)由题意可得f(x)的定义域为(0,+∞),
当a=2时,f(x)=-x2+2x+2(x2-x)lnx,
所以$f'(x)=-2x+2+2(2x-1)lnx+2({x^2}-x)•\frac{1}{x}$=(4x-2)lnx,
由f'(x)>0可得:(4x-2)lnx>0,
所以$\left\{\begin{array}{l}4x-2>0\\ lnx>0\end{array}\right.$或$\left\{\begin{array}{l}4x-2<0\\ lnx<0.\end{array}\right.$,
解得x>1或$0<x<\frac{1}{2}$;
由f'(x)<0可得:(4x-2)lnx<0,
所以$\left\{\begin{array}{l}4x-2>0\\ lnx<0\end{array}\right.$或$\left\{\begin{array}{l}4x-2<0\\ lnx>0\end{array}\right.$,
解得$\frac{1}{2}<x<1$.
综上可知:f(x)递增区间为$(0,\frac{1}{2})$,(1,+∞),递减区间为$(\frac{1}{2},1)$.
(Ⅱ)若x∈(0,+∞)时,f(x)+x2>0恒成立,
则ax+2(x2-x)lnx>0恒成立,
因为x>0,所以a+2(x-1)lnx>0恒成立,
即a>-2(x-1)lnx恒成立,
令g(x)=-2(x-1)lnx,则a>g(x)max.
因为$g'(x)=-2(lnx+\frac{x-1}{x})=-2lnx-2+\frac{2}{x}$,
所以g'(x)在(0,+∞)上是减函数,且g'(1)=0,
所以g(x)在(0,1)上为增函数,在(1,+∞)上是减函数,
∴x=1时,g(x)max=0,
∴a>0,又因为a∈Z,所以amin=1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想,是一道中档题.

 阅读快车系列答案
阅读快车系列答案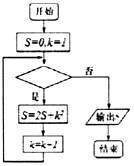
| A. | k≤2? | B. | k≤3? | C. | k≤4? | D. | k≤5? |
| A. | 2米/秒 | B. | 3米/秒 | C. | 4米/秒 | D. | 5米/秒 |
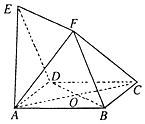 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC,AC、BD交于点O.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC,AC、BD交于点O.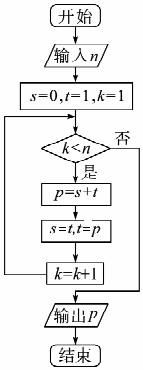
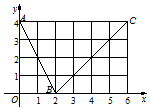 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )