题目内容
设圆C与两圆(x+ )2+y2=4,(x﹣
)2+y2=4,(x﹣ )2+y2=4中的一个内切,另一个外切.
)2+y2=4中的一个内切,另一个外切.
(1)求C的圆心轨迹L的方程;
(2)已知点M( ,
, ),F(
),F( ,0),且P为L上动点,求||MP|﹣|FP||的最大值及此时点P的坐标.
,0),且P为L上动点,求||MP|﹣|FP||的最大值及此时点P的坐标.
 )2+y2=4,(x﹣
)2+y2=4,(x﹣ )2+y2=4中的一个内切,另一个外切.
)2+y2=4中的一个内切,另一个外切.(1)求C的圆心轨迹L的方程;
(2)已知点M(
 ,
, ),F(
),F( ,0),且P为L上动点,求||MP|﹣|FP||的最大值及此时点P的坐标.
,0),且P为L上动点,求||MP|﹣|FP||的最大值及此时点P的坐标.解:(1)两圆的半径都为2,两圆心为F1(﹣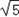 ,0)、F2(
,0)、F2(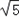 ,0),
,0),
由题意得:|CF1|+2=|CF2|﹣2或|CF2|+2=|CF1|﹣2,
∴||CF2|﹣|CF1||=4=2a<|F1F2|=2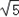 =2c,
=2c,
可知圆心C的轨迹是以原点为中心,焦点在x轴上,且实轴为4,焦距为2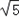 的双曲线,
的双曲线,
因此a=2,c=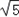 ,则b2=c2﹣a2=1,
,则b2=c2﹣a2=1,
所以轨迹L的方程为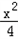 ﹣y2=1;
﹣y2=1;
(2)过点M,F的直线l的方程为y=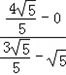 (x﹣
(x﹣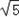 ),
),
即y=﹣2(x﹣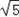 ),代入
),代入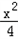 ﹣y2=1,
﹣y2=1,
解得:x1=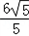 ,x2=
,x2=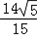 ,
,
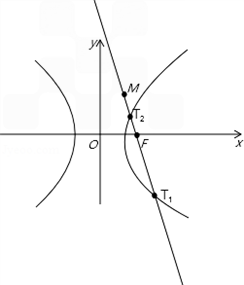
故直线l与双曲线L的交点为T1(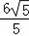 ,﹣
,﹣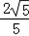 ),T2(
),T2(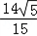 ,
,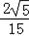 ),
),
因此T1在线段MF外,T2在线段MF内,
故||MT1|﹣|FT1||=|MF|=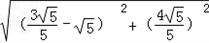 =2,
=2,
||MT2|﹣|FT2||<|MF|=2,
若点P不在MF上,则|MP|﹣|FP|<|MF|=2,
综上所述,|MP|﹣|FP|只在点T1处取得最大值2,此时点P的坐标为(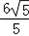 ,﹣
,﹣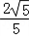 ).
).
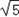 ,0)、F2(
,0)、F2(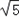 ,0),
,0),由题意得:|CF1|+2=|CF2|﹣2或|CF2|+2=|CF1|﹣2,
∴||CF2|﹣|CF1||=4=2a<|F1F2|=2
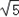 =2c,
=2c,可知圆心C的轨迹是以原点为中心,焦点在x轴上,且实轴为4,焦距为2
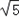 的双曲线,
的双曲线,因此a=2,c=
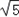 ,则b2=c2﹣a2=1,
,则b2=c2﹣a2=1,所以轨迹L的方程为
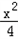 ﹣y2=1;
﹣y2=1;(2)过点M,F的直线l的方程为y=
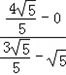 (x﹣
(x﹣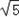 ),
),即y=﹣2(x﹣
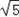 ),代入
),代入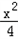 ﹣y2=1,
﹣y2=1,解得:x1=
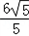 ,x2=
,x2=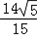 ,
,故直线l与双曲线L的交点为T1(
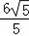 ,﹣
,﹣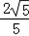 ),T2(
),T2(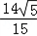 ,
,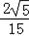 ),
),因此T1在线段MF外,T2在线段MF内,
故||MT1|﹣|FT1||=|MF|=
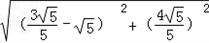 =2,
=2,||MT2|﹣|FT2||<|MF|=2,
若点P不在MF上,则|MP|﹣|FP|<|MF|=2,
综上所述,|MP|﹣|FP|只在点T1处取得最大值2,此时点P的坐标为(
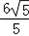 ,﹣
,﹣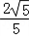 ).
).

练习册系列答案
相关题目
 )2+y2=4,(x-
)2+y2=4,(x- )2+y2=4中的一个内切,另一个外切.
)2+y2=4中的一个内切,另一个外切. ,
, ),F(
),F( ,0),且P为L上动点,求||MP|-|FP||的最大值及此时点P的坐标.
,0),且P为L上动点,求||MP|-|FP||的最大值及此时点P的坐标. )2+y2=4,(x-
)2+y2=4,(x- )2+y2=4中的一个内切,另一个外切.
)2+y2=4中的一个内切,另一个外切. ,
, ),F(
),F( ,0),且P为L上动点,求||MP|-|FP||的最大值及此时点P的坐标.
,0),且P为L上动点,求||MP|-|FP||的最大值及此时点P的坐标. )2+y2=4,(x-
)2+y2=4,(x- )2+y2=4中的一个内切,另一个外切。
)2+y2=4中的一个内切,另一个外切。 ,
, ),F(
),F( ,0)且P为L上动点,求||MP|-|FP||的最大值及此时点P的坐标。
,0)且P为L上动点,求||MP|-|FP||的最大值及此时点P的坐标。