题目内容
16.已知向量$\overrightarrow a$、$\overrightarrow b$满足|$\overrightarrowa}$|=2,|$\overrightarrow b}$|=3,且|2$\overrightarrow a}$-$\overrightarrow b}$|=$\sqrt{13}$,则|2$\overrightarrow a}$+$\overrightarrow b}$|=$\sqrt{37}$向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影为1.分析 首先由已知将|2$\overrightarrow a}$-$\overrightarrow b}$|=$\sqrt{13}$平方,求出向量$\overrightarrow a$,$\overrightarrow b$的数量积,可求|2$\overrightarrow a}$+$\overrightarrow b}$|以及向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影.
解答 解:因为向量$\overrightarrow a$、$\overrightarrow b$满足|$\overrightarrowa}$|=2,|$\overrightarrow b}$|=3,且|2$\overrightarrow a}$-$\overrightarrow b}$|=$\sqrt{13}$,
所以|2$\overrightarrow a}$-$\overrightarrow b}$|2=13,展开得$4{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-4\overrightarrow{a}•\overrightarrow{b}=13$,所以$\overrightarrow{a}•\overrightarrow{b}$=3,
所以向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}=\frac{3}{3}$=1;
则|2$\overrightarrow a}$+$\overrightarrow b}$|2=$4{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+4\overrightarrow{a}•\overrightarrow{b}$=16+9+12=37,所以则|2$\overrightarrow a}$+$\overrightarrow b}$|=$\sqrt{37}$;
故答案为:$\sqrt{37}$;1.
点评 本题考查了平面向量的数量积公式的运用以及一个向量在另一个向量的投影求法;经常考查,注意掌握.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案| A. | 4x-y-1=0 | B. | 3x-4y+1=0 | C. | 3x-4y+1=0 | D. | 4y-3x+1=0 |
| A. | 30° | B. | 60° | C. | 90° | D. | 不能确定 |
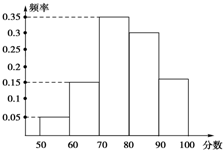 某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图.已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀,且分数为整数)( )
某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图.已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀,且分数为整数)( )