题目内容
11.设函数f(x)=$\frac{1-a}{2}$x2+ax-lnx(a>1).若对任意的a∈(3,4)和任意的x1,x2∈[1,2],恒有$\frac{{a}^{2}-1}{2}$m+ln2>|f(x1)-f(x2)|成立,则实数m的取值范围是m≥$\frac{1}{15}$.分析 先求导函数f′(x),利用导数的正负,确定函数的单调性,得到当a∈(3,4)时,f(x)在[1,2]上单调递减,从而可得|f(x1)-f(x2)|≤f(1)-f(2)=$\frac{a}{2}$对任意a∈(3,4),恒有$\frac{{(a}^{2}-1)}{2}$m+ln2>$\frac{a}{2}$-$\frac{3}{2}$+ln2,等价于m>$\frac{a-3}{{a}^{2}-1}$,求出右边函数的值域,即可求得结论.
解答 解:f′(x)=$\frac{(1-a)(x-\frac{1}{a-1})(x-1)}{x}$,
当 $\frac{1}{a-1}$=1,即a=2时,f′(x)=-$\frac{{(x-1)}^{2}}{x}$≤0,f(x)在(0,+∞)上是减函数;
当 $\frac{1}{a-1}$<1,即a>2时,令f′(x)<0,得0<x<$\frac{1}{a-1}$或x>1;令f′(x)>0,得 $\frac{1}{a-1}$<x<1
当 $\frac{1}{a-1}$>1,即1<a<2时,令f′(x)<0,得0<x<1或x>$\frac{1}{a-1}$;令f′(x)>0,得1<x<$\frac{1}{a-1}$,
综上,当a=2时,f(x)在定义域上是减函数;
当a>2时,f(x)在(0,$\frac{1}{a-1}$)和(1,+∞)上单调递减,在($\frac{1}{a-1}$,1)上单调递增;
当1<a<2时,f(x)在(0,1)和($\frac{1}{a-1}$,+∞)上单调递减,在(1,$\frac{1}{a-1}$)上单调递增;
∴当a∈(3,4)时,f(x)在[1,2]上单调递减
∴当x=1时,f(x)有最大值,当x=2时,f(x)有最小值
∴|f(x1)-f(x2)|≤f(1)-f(2)=$\frac{a}{2}$-$\frac{3}{2}$+ln2
∴对任意a∈(3,4),恒有$\frac{{a}^{2}-1}{2}$m+ln2>$\frac{a}{2}$-$\frac{3}{2}$+ln2
∴m>$\frac{a-3}{{a}^{2}-1}$,构造函数g(a)=$\frac{a-3}{{a}^{2}-1}$,则g′(a)=$\frac{{-(a-3)}^{2}+8}{{{(a}^{2}-1)}^{2}}$,
∵a∈(3,4),∴g′(a)=>0
∴函数g(a)在(3,4)上单调增
∴g(a)∈(0,$\frac{1}{15}$)
∴故答案为:m≥$\frac{1}{15}$.
点评 本题考查导数知识的运用,考查函数的单调性与极值,考查分类讨论的数学思想,考查恒成立问题,分离参数是关键.

| A. | $-\frac{2013}{2014}$ | B. | $-\frac{2014}{2015}$ | C. | $-\frac{2015}{2016}$ | D. | $-\frac{2016}{2017}$ |
 李克强总理4月22日(世界读书日前一天)在厦门大学考察时,指出世界读书日虽然只有一天,但我们应该天天读书,这种好习惯会让我们终身受益.
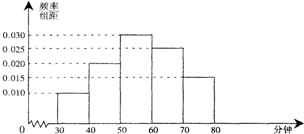
李克强总理4月22日(世界读书日前一天)在厦门大学考察时,指出世界读书日虽然只有一天,但我们应该天天读书,这种好习惯会让我们终身受益.某中学在此期间开展了一系列的读书教育活动.为了解本校学生课外阅读情况,学校随机抽取了100名学生进行调查.右侧是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图.若将日均阅读时间
不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”.
(Ⅰ)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
| 非读书迷 | 读书迷 | 总计 | |
| 男 | 15 | ||
| 女 | 45 | ||
| 总计 |
| P(K2≥k1) | 0.100 | 0.050 | 0.010 | 0.001 |
| k1 | 2.706 | 3.841 | 6.635 | 10.828 |
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.