题目内容
8.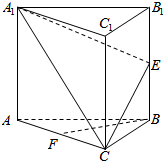 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.(1)求证:BF∥平面A1EC;
(2)求证:平面A1EC⊥平面ACC1A1.
(3)若各棱长相等,求二面角E-AC-B正切值.
分析 (1)连接A1C与AC1交于点O,连接OF,由已知推导出四边形BEOF是平行四边形,由此能证明BF∥平面A1EC.
(2)由已知条件推导出BF⊥AC,OE⊥AC,AA1⊥BF,OE⊥AA1,从而OE⊥平面A1EC,由此能证明平面A1EC⊥平面AA1C1C.
(3)连结AE,BF,由已知得到∠BFE是二面角的平面角,由此能求出二面角E-AC-B正切值.
解答 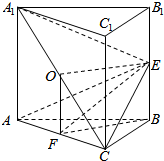 (1)证明:连接A1C与AC1交于点O,连接OF,
(1)证明:连接A1C与AC1交于点O,连接OF,
∵F为AC的中点,∴OF∥C1C,且OF=$\frac{1}{2}$C1C,
∵E为BB1的中点,∴BE∥C1C,且BE=$\frac{1}{2}$C1C,
∴BE∥OF且BE=OF,∴四边形BEOF是平行四边形,
∴BF∥OE,∵BF在平面A1EC外,OE?平面A1EC,
∴BF∥平面A1EC.
(2)证明:∵AB=CB,F为AC的中点,∴BF⊥AC,
由(1)知BF∥OE,∴OE⊥AC,
∵AA1⊥底面ABC,BF?底面ABC,∴AA1⊥BF,
∵BF∥OE,∴OE⊥AA1,
∵AA1∩AC=A,∴OE⊥平面A1EC
∵OE?面A1EC,∴平面A1EC⊥平面AA1C1C.
(3)解:连结AE,BF,
设各棱长为2,由已知得BF=$\sqrt{4-1}$=$\sqrt{3}$,BE=1,AE=CE,
∴EF⊥AC,BF⊥AC,
∴∠BFE是二面角的平面角,
tan∠BFE=$\frac{BE}{BF}$=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
∴二面角E-AC-B正切值为$\frac{\sqrt{3}}{3}$.
点评 本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查二面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | ①② | B. | ①④ | C. | ②④ | D. | ①③ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | (1,2) | B. | (1,3] | C. | (2,3] | D. | (1,3) |
 已知直三棱柱底面各边的比为17:10:9,侧棱长为16cm,全面积为1440cm2,求底面各边之长.(提示:设△ABC的三边长分别为a,b,c,记p=$\frac{1}{2}$(a+b+c),则△ABC的面积S△ABC=$\sqrt{p(p-a)(p-b)(p-c)}$.
已知直三棱柱底面各边的比为17:10:9,侧棱长为16cm,全面积为1440cm2,求底面各边之长.(提示:设△ABC的三边长分别为a,b,c,记p=$\frac{1}{2}$(a+b+c),则△ABC的面积S△ABC=$\sqrt{p(p-a)(p-b)(p-c)}$.
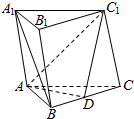 如图,正三棱柱ABC-A1B1C1的各棱均相等,AB=2,D是BC上的一点,AD⊥C1D.
如图,正三棱柱ABC-A1B1C1的各棱均相等,AB=2,D是BC上的一点,AD⊥C1D.