题目内容
函数f(x)=
sin2xsinφ+cos2xcosφ-
sin(
+φ)(0<φ<π),其图象过点(
,
).
(I)求φ的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)的周期与单调递减区间.
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
(I)求φ的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的
| 1 |
| 2 |
(1)由条件知
=
sinφ+
cosφ=
sin(φ+
)
∴φ+
=
?φ=
(2)由(1)代入得
=
sin2x
+
-
=
sin(2x+
)
∴函数g(x)=
sin(4x+
)
∴函数y=g(x)的周期为T=
递减区间为[
+
kπ,
+
kπ]
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
∴φ+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
(2)由(1)代入得
|
=
| 1 |
| 2 |
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
∴函数g(x)=
| 1 |
| 2 |
| π |
| 6 |
∴函数y=g(x)的周期为T=
| π |
| 2 |
递减区间为[
| π |
| 12 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
|

练习册系列答案
相关题目
 函数f(x)=Asin(ωx+?)+b(A>0,ω>0,-
函数f(x)=Asin(ωx+?)+b(A>0,ω>0,-| π |
| 2 |
| π |
| 2 |
A、f(x)=
| ||||
B、f(x)=
| ||||
C、f(x)=
| ||||
D、f(x)=
|
ω为正实数,函数f(x)=
sin
cos
在[-
,
]上为增函数,则( )
| 1 |
| 2 |
| ωx |
| 2 |
| ωx |
| 2 |
| π |
| 3 |
| π |
| 4 |
A、0<ω≤
| ||
| B、0<ω≤2 | ||
C、0<ω≤
| ||
| D、ω≥2 |
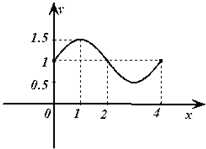 函数f(x)=Asin(ωx+?)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…f(2013)的值分别为( )
函数f(x)=Asin(ωx+?)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…f(2013)的值分别为( )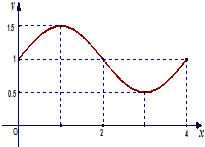 若三角函数f(x)的部分图象如图,则函数f(x)的解析式,以及S=f(1)+f(2)+…+f(2012)的值分别为( )
若三角函数f(x)的部分图象如图,则函数f(x)的解析式,以及S=f(1)+f(2)+…+f(2012)的值分别为( )