题目内容
 如图,分别以矩形ABCD的长为2宽为1,若以1为半径,顶点或边的中点为圆心画圆弧,重叠部分如图中阴影区域,若向该矩形内随机投一点,则该点落在空白区域的概率为( )
如图,分别以矩形ABCD的长为2宽为1,若以1为半径,顶点或边的中点为圆心画圆弧,重叠部分如图中阴影区域,若向该矩形内随机投一点,则该点落在空白区域的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由题意知本题是一个几何概型,试验发生包含的所有事件是矩形面积S=1×2,而满足条件的空白区域可以看作是由四部分组成,每一部分是由边长为1的正方形面积减去半径为1的四分之一圆的面积得到.
解答:解:由题意知本题是一个几何概型,
∵试验发生包含的所有事件是矩形面积S=1×2=2,
空白区域的面积是4(1-
π)=4-π,
∴由几何概型公式得到P=
,
故选A.
∵试验发生包含的所有事件是矩形面积S=1×2=2,
空白区域的面积是4(1-
| 1 |
| 4 |
∴由几何概型公式得到P=
| 4-π |
| 2 |
故选A.
点评:本题考查几何概型,且把几何概型同几何图形的面积结合起来,几何概型和古典概型是高中必修中学习的,高考时常以选择和填空出现,有时文科会考这种类型的解答.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
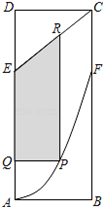
 某矩形花园ABCD,AB=2,
某矩形花园ABCD,AB=2, 某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.
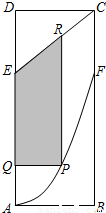
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.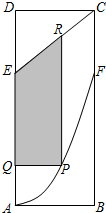 某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.