题目内容
记等比数列{an}的前n项积为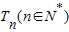 ,已知am-1am+1-2am=0,且T2m-1=128,则m= .
,已知am-1am+1-2am=0,且T2m-1=128,则m= .
【答案】分析:由am-1am+1-2am=0,结合等比数列的性质可得,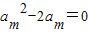 ,从而可求am=2,而T2m-1=a1a2…a2m-1=(a1a2m-1)•(a2a2m-2)…am=
,从而可求am=2,而T2m-1=a1a2…a2m-1=(a1a2m-1)•(a2a2m-2)…am=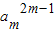 =22m-1,结合已知可求m
=22m-1,结合已知可求m
解答:解:∵am-1am+1-2am=0,
由等比数列的性质可得,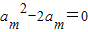
∵am≠0
∴am=2
∵T2m-1=a1a2…a2m-1=(a1a2m-1)•(a2a2m-2)…am
=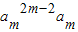 =
=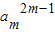 =22m-1=128
=22m-1=128
∴2m-1=7
∴m=4
故答案为4
点评:本题主要考查了等比数列的性质:若m+n=p+q,则am•an=apaq的应用,属于基础试题
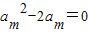 ,从而可求am=2,而T2m-1=a1a2…a2m-1=(a1a2m-1)•(a2a2m-2)…am=
,从而可求am=2,而T2m-1=a1a2…a2m-1=(a1a2m-1)•(a2a2m-2)…am=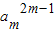 =22m-1,结合已知可求m
=22m-1,结合已知可求m解答:解:∵am-1am+1-2am=0,
由等比数列的性质可得,
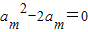
∵am≠0
∴am=2
∵T2m-1=a1a2…a2m-1=(a1a2m-1)•(a2a2m-2)…am
=
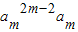 =
=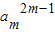 =22m-1=128
=22m-1=128∴2m-1=7
∴m=4
故答案为4
点评:本题主要考查了等比数列的性质:若m+n=p+q,则am•an=apaq的应用,属于基础试题

练习册系列答案
相关题目
记等比数列{an}的前n项和为Sn,若S3=2,S6=18,则
等于( )
| S10 |
| S5 |
| A、-3 | B、5 | C、-31 | D、33 |