题目内容
F(-c,0)是双曲线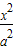 -
-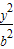 =1(a>0,b>0)的左焦点,P是抛物线y2=4cx上一点,直线FP与圆x2+y2=a2相切于点E,且PE=FE,若双曲线的焦距为2
=1(a>0,b>0)的左焦点,P是抛物线y2=4cx上一点,直线FP与圆x2+y2=a2相切于点E,且PE=FE,若双曲线的焦距为2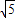 +2,则双曲线的实轴长为( )
+2,则双曲线的实轴长为( )A.4
B.2
C.
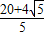
D.
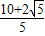
【答案】分析:确定∠FPF2=90°,根据△FEO∽△FPF2,可得PF2=2a,过F作x轴的垂线l,过P作PQ⊥l于Q,则PQ=PF2=2a,利用Rt△FPQ∽Rt△F2FQ,在Rt△FEO中,利用勾股定理,双曲线的焦距为2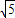 +2,建立方程,从而可求双曲线的实轴长.
+2,建立方程,从而可求双曲线的实轴长.
解答:解:抛物线y2=4cx的焦点F2(c,0)
∵E为直线FP与以原点为圆心a为半径的圆的切点,PE=EF
∴OE为直线FP的中垂线 (O为原点)
∴OP=OF=c
又FF2=2c,O为FF2中点,OP=c
∴∠FPF2=90°(直角三角形中,直角顶点与斜边中点的连线长度为斜边的一半)
根据△FEO∽△FPF2,可得
∵EO=a,∴PF2=2a
过F作x轴的垂线l,过P作PQ⊥l于Q,则PQ=PF2=2a
又Rt△FPQ∽Rt△F2FQ,令PF=2x=2EF,∴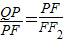 ,即
,即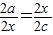 ,即x2=ac=EF2
,即x2=ac=EF2
∴在Rt△FEO中,OF2=EF2+EO2,即c2=ac+a2
∵双曲线的焦距为2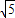 +2,
+2,
∴a2+(1+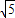 )a-(1+
)a-(1+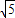 )2=0
)2=0
∴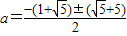
∴a1=2,a2=- -3 (舍)
-3 (舍)
∴实轴长为4
故选A.
点评:本题考查圆锥曲线的综合,考查双曲线的几何性质,考查学生分析解决问题的能力,综合性强.
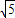 +2,建立方程,从而可求双曲线的实轴长.
+2,建立方程,从而可求双曲线的实轴长.解答:解:抛物线y2=4cx的焦点F2(c,0)
∵E为直线FP与以原点为圆心a为半径的圆的切点,PE=EF
∴OE为直线FP的中垂线 (O为原点)
∴OP=OF=c
又FF2=2c,O为FF2中点,OP=c
∴∠FPF2=90°(直角三角形中,直角顶点与斜边中点的连线长度为斜边的一半)
根据△FEO∽△FPF2,可得

∵EO=a,∴PF2=2a
过F作x轴的垂线l,过P作PQ⊥l于Q,则PQ=PF2=2a
又Rt△FPQ∽Rt△F2FQ,令PF=2x=2EF,∴
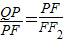 ,即
,即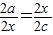 ,即x2=ac=EF2
,即x2=ac=EF2∴在Rt△FEO中,OF2=EF2+EO2,即c2=ac+a2
∵双曲线的焦距为2
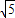 +2,
+2,∴a2+(1+
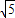 )a-(1+
)a-(1+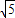 )2=0
)2=0∴
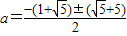
∴a1=2,a2=-
 -3 (舍)
-3 (舍)∴实轴长为4
故选A.
点评:本题考查圆锥曲线的综合,考查双曲线的几何性质,考查学生分析解决问题的能力,综合性强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
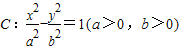 的右焦点,若双曲线C的渐近线与圆
的右焦点,若双曲线C的渐近线与圆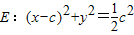 相切,则双曲线C的离心率为 .
相切,则双曲线C的离心率为 .