题目内容
过椭圆 的右焦点F作斜率为k(k>0)的直线l与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足:
的右焦点F作斜率为k(k>0)的直线l与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足:
(I)证明点A和点B分别在第一、三象限;
(II)若
 的取值范围.
的取值范围.
【答案】分析:(I)设直线方程为y=k(x-2),由 及k>0,可知
及k>0,可知 设A(x1,y1),B(x2,y2),则A、B坐标是方程组
设A(x1,y1),B(x2,y2),则A、B坐标是方程组 的解,
的解,
消去y得(1+3k2)x2-12k2x+12k2-6=0,再由根与系数的关系可以判断出A、B分别在第一、三象限.
(II)由 ,能够推导出k的取值范围.
,能够推导出k的取值范围.
解答:解:(I)由已知, ,直线方程为y=k(x-2),由
,直线方程为y=k(x-2),由 及k>0,得
及k>0,得 ,解这个不等式,得
,解这个不等式,得
设A(x1,y1),B(x2,y2),则A、B坐标是方程组 的解,
的解,
消去y得(1+3k2)x2-12k2x+12k2-6=0,则 ,
,
y1y2=k(x1-2)•k(x2-2)=k2[x1x2-2(x1+x2)+4]
= ,
,
∵ ,
,
不妨设x1<0,则x2>0,此时y1=k(x1-2)<0,于是y2>0,
A、B分别在第一、三象限.
(II)由 ,
,
注意到 所以k的取值范围是
所以k的取值范围是
点评:本题综合考查直线和椭圆的位置关系,解题时要认真审题,注意公式的灵活运用.
 及k>0,可知
及k>0,可知 设A(x1,y1),B(x2,y2),则A、B坐标是方程组
设A(x1,y1),B(x2,y2),则A、B坐标是方程组 的解,
的解,消去y得(1+3k2)x2-12k2x+12k2-6=0,再由根与系数的关系可以判断出A、B分别在第一、三象限.
(II)由
 ,能够推导出k的取值范围.
,能够推导出k的取值范围.解答:解:(I)由已知,
 ,直线方程为y=k(x-2),由
,直线方程为y=k(x-2),由 及k>0,得
及k>0,得 ,解这个不等式,得
,解这个不等式,得
设A(x1,y1),B(x2,y2),则A、B坐标是方程组
 的解,
的解,消去y得(1+3k2)x2-12k2x+12k2-6=0,则
 ,
,y1y2=k(x1-2)•k(x2-2)=k2[x1x2-2(x1+x2)+4]
=
 ,
,∵
 ,
,不妨设x1<0,则x2>0,此时y1=k(x1-2)<0,于是y2>0,
A、B分别在第一、三象限.
(II)由
 ,
,注意到
 所以k的取值范围是
所以k的取值范围是
点评:本题综合考查直线和椭圆的位置关系,解题时要认真审题,注意公式的灵活运用.

练习册系列答案
相关题目
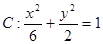 的右焦点F作斜率为
的右焦点F作斜率为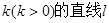 与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足:
与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足: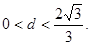
 的取值范围。
的取值范围。 的右焦点F作斜率为k(k>0)的直线l与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足:
的右焦点F作斜率为k(k>0)的直线l与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足:
 的取值范围.
的取值范围.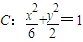 的右焦点F作斜率为k(k>0)的直线l与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足:
的右焦点F作斜率为k(k>0)的直线l与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足: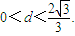
 的取值范围.
的取值范围.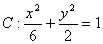 的右焦点F作斜率为
的右焦点F作斜率为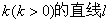 与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足:
与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足: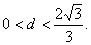
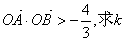 的取值范围。
的取值范围。