题目内容
 已知椭圆
已知椭圆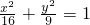 与x轴交于A、B两点,焦点为F1、F2.
与x轴交于A、B两点,焦点为F1、F2.
(1)求以F1、F2为顶点,以A、B为焦点的双曲线E的方程;
(2)M为双曲线E上一点,y轴上一点P  ,求|MP|取最小值时M点的坐标.
,求|MP|取最小值时M点的坐标.
解:(1)设双曲线方程为
则a2=7 b2=16∴b2=9…(3分)
所求双曲线方程: …(6分)
…(6分)
(2)设M(x,y),
 =
= =
= …(9分)
…(9分)
当y=3时,|MP|2最小,|MP|最小.
代入方程得, …(12分)
…(12分)
分析:(1)通过双曲线方程求出焦点坐标与顶点,即可求出以F1、F2为顶点,以A、B为焦点的双曲线E的方程;
(2)设出M坐标,直接利用两点间的距离公式求出|MP|的表达式,代入双曲线方程,直接利用二次函数求出表达式取得最小值时M点的坐标.
点评:本题是中档题,考查双曲线方程的应用,双曲线才的求法,二次函数最值的求法,考查计算能力,转化思想的应用.

则a2=7 b2=16∴b2=9…(3分)
所求双曲线方程:
 …(6分)
…(6分)(2)设M(x,y),
 =
= =
= …(9分)
…(9分)当y=3时,|MP|2最小,|MP|最小.
代入方程得,
 …(12分)
…(12分)分析:(1)通过双曲线方程求出焦点坐标与顶点,即可求出以F1、F2为顶点,以A、B为焦点的双曲线E的方程;
(2)设出M坐标,直接利用两点间的距离公式求出|MP|的表达式,代入双曲线方程,直接利用二次函数求出表达式取得最小值时M点的坐标.
点评:本题是中档题,考查双曲线方程的应用,双曲线才的求法,二次函数最值的求法,考查计算能力,转化思想的应用.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 已知椭圆
已知椭圆 与x轴交于A、B两点,焦点为F1、F2.
与x轴交于A、B两点,焦点为F1、F2. ,求|MP|取最小值时M点的坐标.
,求|MP|取最小值时M点的坐标.
 与x轴交于A、B两点,焦点为F1、F2.
与x轴交于A、B两点,焦点为F1、F2. (1)求以F1、F2为顶点,以A、B为焦点的双曲线E的方程;
(1)求以F1、F2为顶点,以A、B为焦点的双曲线E的方程; ,求│MP│取最小值时M点的坐标.
,求│MP│取最小值时M点的坐标.