题目内容
若G是△ABC的重心,D、E、F分别是AB、BC、CA的中点,则
等于( ) A.6
?? B.-6?
?
C.-6
? D.0
解析:由于G是△ABC的重心,想到可利用三角形重心的性质:三角形的重心到一个顶点的距离与它到这个顶点对边中点的距离比是2∶1.在此题中也即|AG|∶|GE|=|BG|∶|GF|=?|CG|∶|GD|=2∶1,由此可知
||=2||,||=2|
|,|
|=2|
|,由此知
=2
,
=2
,
=2
,因此
.接下来关键是寻找
、
、
的关系.?
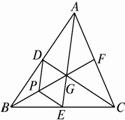
如图,令GB的中点为P,连结DP、PE,得平行四边形GDPE.取向量
、
为一组基底,则有
=2
=2(
+
),
=-2
,
=-2
,上面三式两端分别相加,有
=0.?
∴应选D.
答案:D
练习册系列答案
名校课堂系列答案
相关题目
设P是△ABC内任意一点，S△ABC表示△ABC的面积，λ1=
，λ2=
，λ3=
，定义f（P）=（λ1，λ2，λ3），若G是△ABC的重心，f（Q）=（
，
，
），则（ ）
| S△PBC |
| S△ABc |
| S△PCA |
| S△ABC |
| S△PAB |
| S△ABC |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| A、点Q在△GAB内 |
| B、点Q在△GBC内 |
| C、点Q在△GCA内 |
| D、点Q与点G重合 |
,λ2=
,λ3=
,定义f(P)=(λ1,λ2,λ3),若G是△ABC的重心,f(Q)=(
, 
, 
),则( )
，λ2=
,λ3=
，定义f（P）=（λ1，λ2，λ3）.若G是△ABC的重心，f（Q）=（
,
，
），则（ ）
，λ2＝
，λ3＝
，定义
，
，
），则
， λ2＝
，λ3＝
，定义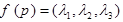
,若G是△ABC的重心，f（Q）＝（
，
，
），则