题目内容
若随机向一个边长为1的正三角形内丢一粒豆子(假设该豆子一定落在三角形内),则豆子落在此三角形内切圆内的概率是
.
| ||
| 9 |
| ||
| 9 |
分析:由于三角形的边长为1,则内切圆半径为
,然后求出三角形面积及其内切圆的面积,代入几何概型公式,即可得到答案.
| ||
| 6 |
解答:解:∵正三角形的边长为1,
∵正三角形的面积S三角形=
×12=
其内切圆半径为
,内切圆面积S圆=πr2=
π
故向正三角形内撒一粒豆子,则豆子落在圆内的概率P=
=
.
故答案为:
.
∵正三角形的面积S三角形=
| ||
| 4 |
| ||
| 4 |
其内切圆半径为
| ||
| 6 |
| 1 |
| 12 |
故向正三角形内撒一粒豆子,则豆子落在圆内的概率P=
| S圆 |
| S正三角形 |
| ||
| 9 |
故答案为:
| ||
| 9 |
点评:本题主要考查了几何概型,以及圆与正三角形的面积的计算,解题的关键是弄清几何测度,属于基础题.

练习册系列答案
相关题目
(本小题满分14分)
 Monte-Carlo方法在解决数学问题中有广泛的应用。下面是利用Monte-Carlo方法来计算定积分。考虑定积分
Monte-Carlo方法在解决数学问题中有广泛的应用。下面是利用Monte-Carlo方法来计算定积分。考虑定积分![]() ,这时
,这时![]() 等于由曲线
等于由曲线![]() ,
,![]() 轴,
轴,![]() 所围成的区域M的面积,为求它的值,我们在M外作一个边长为1正方形OABC。设想在正方形OABC内随机投掷
所围成的区域M的面积,为求它的值,我们在M外作一个边长为1正方形OABC。设想在正方形OABC内随机投掷![]() 个点,若
个点,若![]() 个点中有
个点中有![]() 个点落入
个点落入![]() 中,则
中,则![]() 的面积的估计值为
的面积的估计值为![]() ,此即为定积分
,此即为定积分![]() 的估计值I。向正方形
的估计值I。向正方形![]() 中随机投掷10000个点,有
中随机投掷10000个点,有![]() 个点落入区域M
个点落入区域M
(1)若![]() =2099,计算I的值,并以实际值比较误差是否在5%以内
=2099,计算I的值,并以实际值比较误差是否在5%以内
(2)求![]() 的数学期望
的数学期望
(3)用以上方法求定积分,求I与实际值之差在区间(—0.01,0.01)的概率
附表:![]()
| n | 1899 | 1900 | 1901 | 2099 | 2100 | 2101 |
| P(n) | 0.0058 | 0.0062 | 0.0067 | 0.9933 | 0.9938 | 0.9942 |
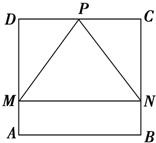 如图,四边形ABCD是一个边长为1的正方形,△MPN是正方形的一个内接正三角形,且MN∥AB,若向正方形内部随机投入一个质点,则质点恰好落在△MPN的概率为( )
如图,四边形ABCD是一个边长为1的正方形,△MPN是正方形的一个内接正三角形,且MN∥AB,若向正方形内部随机投入一个质点,则质点恰好落在△MPN的概率为( )