题目内容
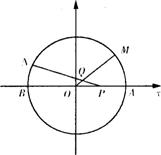
如图, 是半径为a的半圆,AC为直径,点E为
是半径为a的半圆,AC为直径,点E为 的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=
的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD= a,FE=
a,FE= a,
a,
(Ⅰ)证明:EB⊥FD;
(Ⅱ)已知点Q,R分别为线段FE,FB上的点,使得FQ= FE,FR=
FE,FR= FB,求平面BED与平面RQD所成二面角的正弦值。
FB,求平面BED与平面RQD所成二面角的正弦值。
 是半径为a的半圆,AC为直径,点E为
是半径为a的半圆,AC为直径,点E为 的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=
的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD= a,FE=
a,FE= a,
a,(Ⅰ)证明:EB⊥FD;
(Ⅱ)已知点Q,R分别为线段FE,FB上的点,使得FQ=
 FE,FR=
FE,FR= FB,求平面BED与平面RQD所成二面角的正弦值。
FB,求平面BED与平面RQD所成二面角的正弦值。 
(Ⅰ)证明:∵E为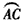 的中点,AB=BC,AC为直径, 的中点,AB=BC,AC为直径,∴EB⊥AD, 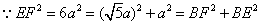 , ,∴EB⊥FB, 又∵BF∩BD=B, ∴EB⊥平面BDF, ∵FD 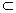 平面BDF, 平面BDF,∴EB⊥FD; |
|
(Ⅱ)解:过D作HD∥QR,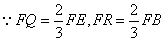 , ,∴QR∥EB,∴HD∥EB, 又∵D∈平面BED∩平面RQD, ∴HD为平面BED与平面RQD的交线, ∵BD,RD 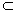 平面BDF,EB⊥平面BDF, 平面BDF,EB⊥平面BDF,∴HD⊥BD,HD⊥RD, ∴∠RDB为平面BED与平面RQD所成二面角的平面角, ∵FB=FD,BC=CD, ∴FC⊥BD, ∴ 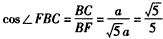 , ,∴ 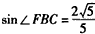 , ,∴ 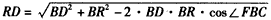 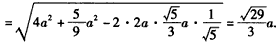 , ,∴ 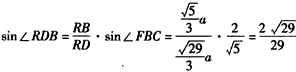 。 。 |
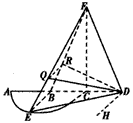 |

练习册系列答案
相关题目
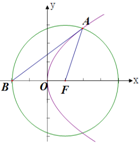 (2012•泉州模拟)如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.
(2012•泉州模拟)如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F. (2009•黄浦区一模)如图所示,点A、B是单位圆(圆心在原点,半径为1的圆)上两点,OA、OB与x轴正半轴所成的角分别为α和-β.
(2009•黄浦区一模)如图所示,点A、B是单位圆(圆心在原点,半径为1的圆)上两点,OA、OB与x轴正半轴所成的角分别为α和-β. 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长.
 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长. ,其中
,其中 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的极坐标方程为
的极坐标方程为 ,
, 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长. ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程; 满足
满足 ,求
,求 的最小值;
的最小值;