题目内容
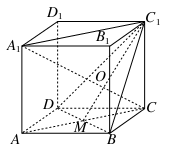
如图,已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点。
(1)求证:直线AB1∥平面C1DB;
(2)求异面直线AB1与BC1所成角的余弦值
(1)见解析;(2) 。
。
解析试题分析:(1) 连B C交
C交 于E,连DE, 要证直线AB1∥平面C1DB,证明AB1∥DE即可;(2)根据异面直线所成角的定义并结合(1)可知∠DEB为异面直线
于E,连DE, 要证直线AB1∥平面C1DB,证明AB1∥DE即可;(2)根据异面直线所成角的定义并结合(1)可知∠DEB为异面直线 所成的角,然后用余弦定理求解。
所成的角,然后用余弦定理求解。
试题解析:(1)连B C交
C交 于E,连DE, 则DE∥
于E,连DE, 则DE∥ ,
,
而DE 面C
面C DB,
DB,
 面C
面C DB, ∴
DB, ∴ 平面C1DB。
平面C1DB。
(2)由(1)知∠DEB为异面直线 所成的角,
所成的角,
在
由余弦定理得 。
。
考点:(1)线面平行判断定理的应用;(2)异面直线所成角的定义;(3)余弦定理的应用。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点。
的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点。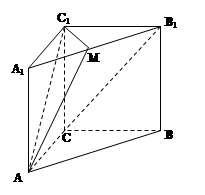

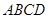 中,
中, ,
,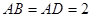 ,
,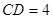 ,点
,点 为线段
为线段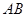 上异于
上异于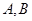 的点,且
的点,且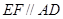 ,沿
,沿 将面
将面 折起,使平面
折起,使平面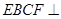 平面
平面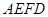 ,如图2.
,如图2.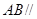 平面
平面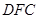 ;
;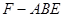 体积最大时,求平面
体积最大时,求平面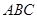 与平面
与平面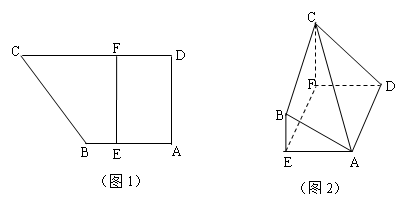

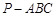 中,点
中,点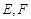 分别是棱
分别是棱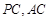 的中点.
的中点. 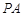 //平面
//平面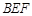 ;
; 平面
平面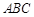 ,
,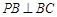 ,求证:
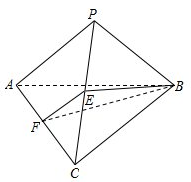
,求证: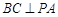 .
.
 的高为
的高为 ,底面
,底面 是边长为
是边长为 的正方形,顶点
的正方形,顶点 在底面上的射影是正方形
在底面上的射影是正方形 .
. 是棱
是棱 的中点.试求直线
的中点.试求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
,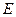 分别是
分别是 的中点,
的中点, .
. ;
; ;
; 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.